Question

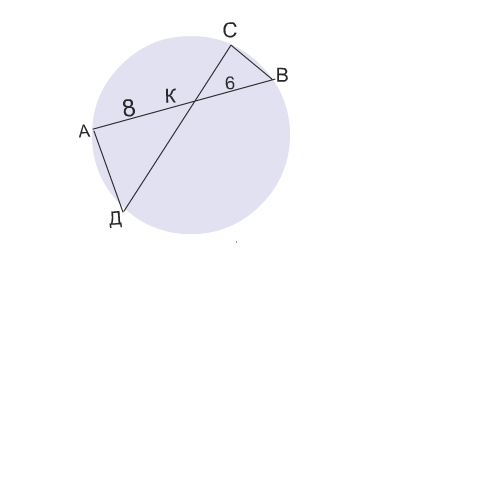
в окружности проведены хорды AB и CD,пересекающиеся в точке K,AK=8 см,BK=6 см.Площадь треугольника AKD равна 128 см в квадрате.Найдите площадь треугольника CBK.

Answer 1

Рассмотрим треугольники АКД и СКВ.

В них все углы равны:

Углы при К -как вертикальные. 

Углы ДСВ и ДАВ - как опирающиеся на одну дугу.

Углы АДС и СВА - тоже опираются на одну и ту же дугу и равны

Отсюда Δ АКД  ≈ Δ СКВ

Коэффициент подобия k в них найдем отношением сторон, противолежащих равным углам. 

k=КВ:АК=6/8 или 3/4

Отношение площадей подобных треугольников равно квадрату коэффициента их подобия. 

S Δ АКД :SΔ СВК= k²

SΔ СВК:128=9:16

128·9=16 SΔ СВК

1152=16SΔ СВК 

SΔ СВК=1152:16=72 см²