Предмет: Геометрия,
автор: Опечатка
Есть тут хоть одна геометрическая умняша? Сразу предупреждаю, на халяву ни шиша вы не получите.
Задача:
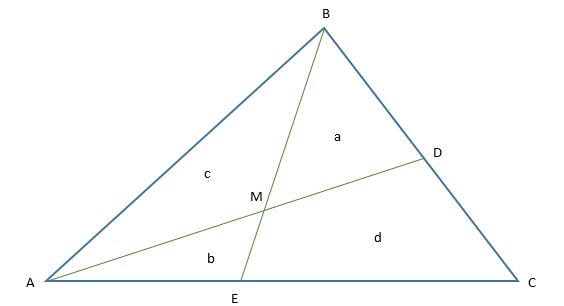
В треугольнике ABC проведены две чевианы AD и BE. Они пересекаются в
точке M. Площадь треугольника AME равна b, треугольника BMD равна а,
треугольника AMB - с. Найти площадь треугольника ABC.
Выходная формула: Sabc=a+b+c+a*b/c+(a+a*b/c)*(b+a*b/c)/(c-a*b/c)
Объясните поэтапно вывод формулы
Ответы
Автор ответа:
0
По свойству чевианы (если надо, его можно легко доказать):


Вот и вся геометрия. Имеем два ур-я с двумя неизвестными. Из первого находим одно, подставляем во второе.

Подставляем



Дальше дело техники
Решение прекращено по согласованию с автором вопроса
Вот и вся геометрия. Имеем два ур-я с двумя неизвестными. Из первого находим одно, подставляем во второе.
Подставляем
Дальше дело техники
Решение прекращено по согласованию с автором вопроса
Приложения:
Автор ответа:
0
чёрт, ну как сделать лучшим? :D
Автор ответа:
0
Ну там надпись есть, надо нажать на не))
Автор ответа:
0
ок, спасибо огроменное :D
Похожие вопросы
Предмет: Биология,
автор: mogadi5093
Предмет: География,
автор: jdjsjdbsbshsnsbsbbsb
Предмет: Українська мова,
автор: malayairka
Предмет: Математика,
автор: misskocheeva
Предмет: География,
автор: dbiersieniov