Предмет: Математика,
автор: reagan11
Помогите!! очень срочно!!
Приложения:
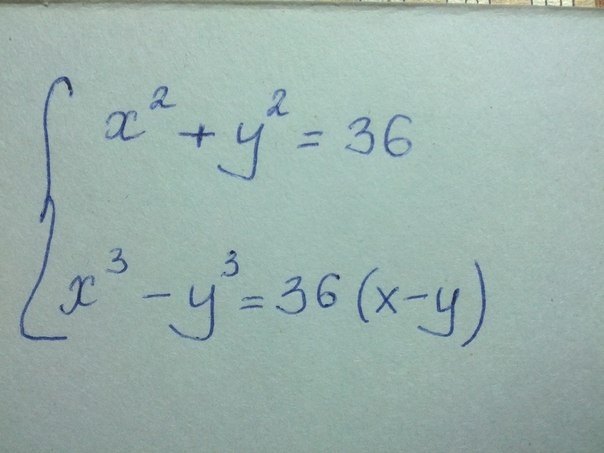
Ответы
Автор ответа:
0
Вычтем из второго уравнения первое, первое оставим неизменным
xy=0, значит либо x=0, либо y=0. Вариант x=0 и y=0 не рассматриваем, т.к. в этом случае первое уравнение системы не выполняется. Получаем две системы
Имеем 4 решения: (0; -6), (0; 6), (-6; 0), (6; 0).
Похожие вопросы
Предмет: Другие предметы,
автор: harleyrocklov2e
Предмет: Геометрия,
автор: halitaliev
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: zoyagordeeva1