Question

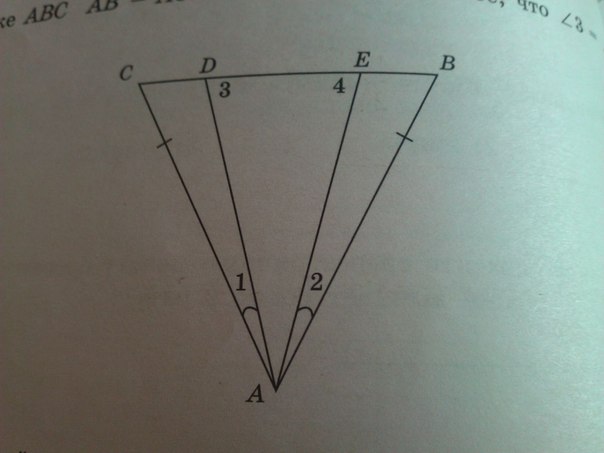
В треугольнике АВС АВ=АС  и угол 1= углу 2. Докажите, что угол 3= углу 4

Answer 1

если треугольник равнобедренный, то В=С, угол 3=1+ С, как внешний для треуг АСД, аналогично, 4=2+В. Значит 3=4 как суммы соответственно равных углов.

Answer 2

Так как треугольник АВС равнобедренный АС= АВ, то углы при вершинах С и В равны. 
Треугольники АDC и АЕВ равны по 2 признаку равенства треугольников. 
(АD=AE, угол1=углу2, уголС=углуВ) 
Значит треугольник АDЕ равнобедренный и углы при основании DЕ равны угол 3 = углу4.