Предмет: Алгебра,
автор: vfhbyf1
помогите решить : вычислить предел
Приложения:
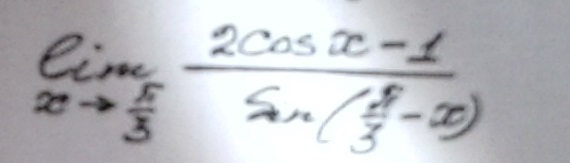
Ответы
Автор ответа:
0
2 способ. Правило Лопиталя.
Автор ответа:
0
Применили формулу разности косинусов cosa-cosb=...
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Геометрия,
автор: barsgames
Предмет: История,
автор: renat8701
Предмет: Биология,
автор: вво
Предмет: Физика,
автор: kristianna5