Question

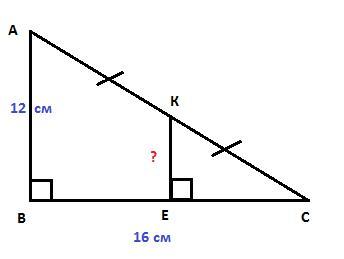
В треугольнике ABC угол B прямой AB =12см, BC =16см, K середина стороны AC из точки K опущен перпендикуляр KE к стороне BC найдите KE

Answer 1

См. рисунок.

За теоремой Пифагора найдём сторону AC:

$AC=sqrt{AB^2+BC^2}=sqrt{12^2+16^2}=sqrt{144+256}=sqrt{400}=20$ см.

Тогда AK=KC=10 см.

$triangle ABC sim triangle KEC =>frac{AB}{KE}=frac{BC}{EC}=frac{AC}{KE}\\frac{AB}{KE}=frac{AC}{KE}=>frac{12}{KE}=frac{20}{10}=>KE=frac{120}{20}=6$

Треугольники подобны по 1 признаку ( ∠BAC=∠EKC, ∠ACB=∠KCE)

ОТВЕТ: 6 см.

Answer 2

AB⊥BC, KE⊥BC  ⇒  AB║KE  как два перпендикуляра к одной прямой.

По теореме Фалеса : AK = KC  ⇒  BE = EC  ⇒

KE - средняя линия ΔABC, KE║AB   ⇒

KE = AB : 2 = 12 : 2 = 6 см

Ответ: KE = 6 см