Через катет равнобедренного прямоугольного треугольника проведена пласкость альфа. Угол между плоскостями треугольника и альфа равен 60'. Вычислите длины проекций сторон данного треугольника на плоскость альфа, если длина катета данного треугольника равна 10 дм.
Ответы
(Дано решение для угла между плоскостями, равного 60°) Пусть данный треугольник АВС, угол С=90°, АС=ВС=10 см, катет ВС принадлежит плоскости α.
Угол между двумя плоскостями равен линейному углу между двумя лучами, проведенными в этих плоскостях перпендикулярно к одной точке на прямой, принадлежащей обеим плоскостям.
Перпендикуляр, опущенный из точки на плоскость, перпендикулярен любой прямой, лежащей в этой плоскости
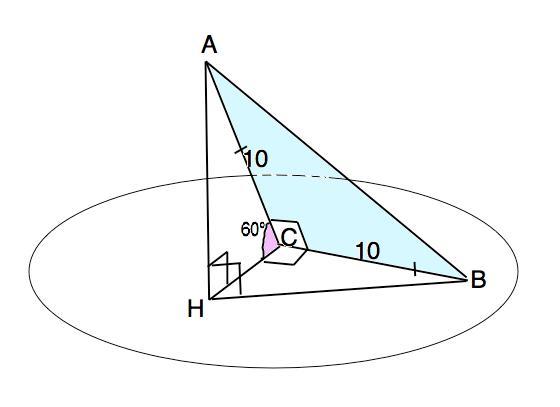
Опустим перпендикуляр АН на плоскость α (см. рисунок). АС - наклонная, НС - её проекция. Угол НСВ по т. о 3-х перпендикулярах равен 90°.⇒ ∆ АСН и ∆ АНВ – прямоугольные.
По условию угол АСН=60° ⇒ НС=АС•cos 60°=10•1/2=5 дм. - это проекция катета АС на плоскость α.
НВ - проекция АВ на плоскость α. По т.Пифагора ВН=√(CH²+CB²)=√(25+100)=5√5 дм