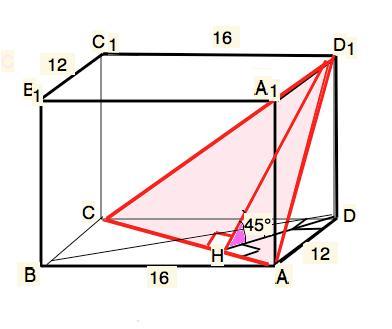
В прямоугольном параллелепипеде ABCDA1B1C1D1 проведено сечение плоскостью, содержащей прямую AC и вершину D1. Угол можду плоскостями сечения и основания равен 45'. Стороны основания параллелепипеда равны 12 дм и 16 дм. вычислите площадь сечения.
Ответы
Итак... угол DOD1 = 45 градусов, . В стреугльника DOD1 угол D = 90 градусов, => треугольник DOD1 = прямоугольный => угол DOD1 = углу OD1D => OD = DD1 = H. OD = 1/2 * DB = 1/2* корень из( 144 + 256) = 1/2 * 20 = 10. Найдем площадь сечения через формулу 1/2 * OD1 * AC. AC = 20, OD1 = корень из(100+100) = 10√2 => S ACD1 = 1/2 * 20 * 10√2 = 100√2... Кажется я что-то личшнее написал:)
Ответ: 96√2 дм²
Объяснение: Угол между плоскостями – двугранный угол. Его величина определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём. На рисунке вложения данный угол образован наклонной D1H и её проекцией НD. Оба отрезка перпендикулярны АС, а угол D1HD=45° по условию. Треугольник D1HD прямоугольный, т.к. параллелепипед прямоугольный и ребро DD1 перпендикулярно плоскости основания.
По т.Пифагора АС=√(CD²+ DA²)=√(16²+12²)=20 дм.
DH=CD•AD:AC=16•12:20=9,6 дм
В ∆ АСD1 по т.Пифагора из ∆ DHD1 высота D1H=DH:cos45° D1H==9,6(√2/2)=9,6√2.
S(ACD1)=D1H•AC:2=96√2 дм²