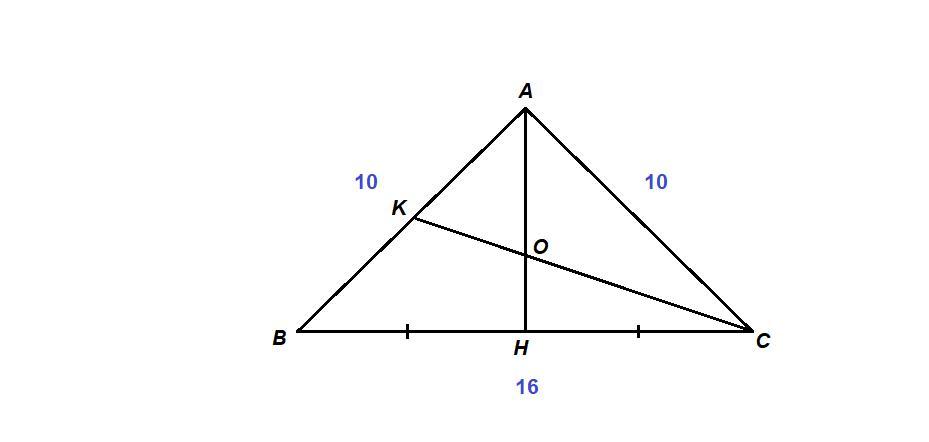
Найдите расстояние от точки пересечения медиан равнобедренного треугольника АВС до стороны ВС, если АВ = АС = 10 см, ВС = 16 см.
Ответы
Треугольник АВС - равнобедренний, то Медиана АК является и высотой. ВК=КС=8, т.к. ВС=16. Поэтому треугольник АВК - прямоугольный, АК= Корень( AB^2-KC^2)=корень( 100-64)=6.
Медианы в точке пересечения делятся в отношении 2:1, то ОК=1/3*АК=1/3*6=2
Ответ. 2 см.
Ответ: 2 см
Объяснение:
АН и СК - медианы.
АН - медиана, проведенная к основанию равнобедренного треугольника, значит АН и высота.
О - точка пересечения медиан, ОН - искомое расстояние.
ВН = НС = 1/2 ВС = 8 см
ΔАВН: ∠АНВ = 90°, по теореме Пифагора:
АН = √(АВ² - ВН²) = √(10² - 8²) = √(100 - 64) = √36 = 6 см
Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины, значит
ОН = 1/3 АН = 1/3 · 6 = 2 см