Предмет: Геометрия,
автор: zheka95
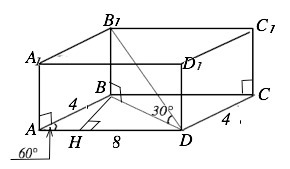
Основание прямой призмы АВСДА1В1С1Д1 является параллелограмм АВСД со сторонами 4 см и 8 см и углом, равным 60". Диагональ В1Д призмы образует с плоскостью основания угол 30. Найдите площадь боковой поверхности призмы
Ответы
Автор ответа:
0
На рисунке в приложении ВН - высота параллелограмма АВСD (основания призмы).
ВН=АВ•sin60°=4•√3/2=2√3
АН=АВ•cos60°=4•1/2=2 см
HD=AD-AH=8-2=6 см
Диагональ основания BD=√(BH²+HD²)=√48=4√3
Высота призмы ВВ1=BD:ctg30°=4√3/√3=4 см
Площадь боковой поверхности прямой призмы равна произведению её бокового ребра (высоты) на периметр Р основания
S (бок)=Н•Р=4•2•(4+8)=8•12=96 см²
---------
BD можно найти и по т.косинусов.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: zldyzkalieva
Предмет: Другие предметы,
автор: anvartursunzanov736
Предмет: Химия,
автор: linalinakizub
Предмет: Физика,
автор: люблюсебяочень