Question

Основание пирамиды - ромб со стороной 16см и углом 30 °. Все двугранные углы при ребрах основания составляют 60 °. Найти объем пирамиды.

Answer 1

Основание пирамиды - ромб со стороной 16см и углом 30 °. Все двугранные углы при ребрах основания составляют 60 °. Найти объем пирамиды.
--------------
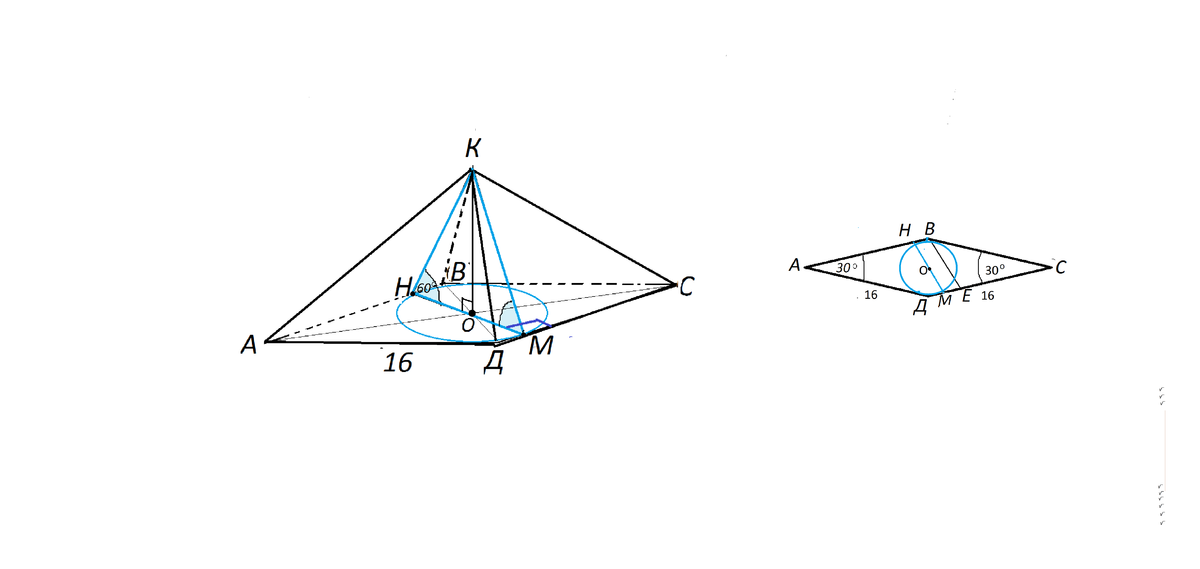
Если все грани наклонены к основанию под равным углом,
основание О высоты КО пирамиды находится в центре вписанной в основание окружности.
Высота  ВЕ  ромба в основании равна половине его стороны, т.к. противолежит углу 30 градусов.
ВЕ=16:2=8
Высоту КО пирамиды найдем из прямоугольного треугольника КОМ
Диаметр вписанной окружности НМ равен высоте ромба ( основания)=8см
Отрезок ОМ равен радиусу вписанной окружности ( половине высоты ромба) и равен 4 см
угол КМО=60°⇒угол ОКМ=30°
КО=ОМ:tg (30°)=4√3 
V=SH:3
S=АВ*МЕ=16*8=128
V=(128*4√3):3=512√3
------------
[email protected]