Question

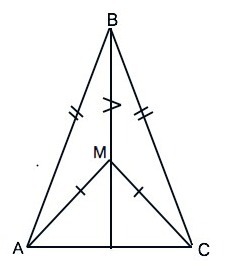
На стороне АС как на основании построены по одну сторону от нее два равнобедренных треугольника АВС и АМС. Докажите, что прямая ВМ пересекает сторону АС в ее середине.

Answer 1

Треугольники АВС и АМС - равнобедренные.

Поэтому в ∆ ВАМ и ∆ ВСМ стороны АВ=СB; AМ=СМ, сторона ВМ - общая.⇒

∆ ВАМ =∆ ВСМ по 3-му признаку равенства треугольников.

Из равенства треугольников следует равенство их сходственных углов.

∠AВМ=∠СВМ, следовательно, прямая ВМ - биссектриса угла В ∆ АВС и по свойству биссектрисы равнобедренного треугольника является его высотой и медианой. ⇒

Прямая ВМ пересекает основание АС равнобедренного ∆ АВС в его середине.