Question

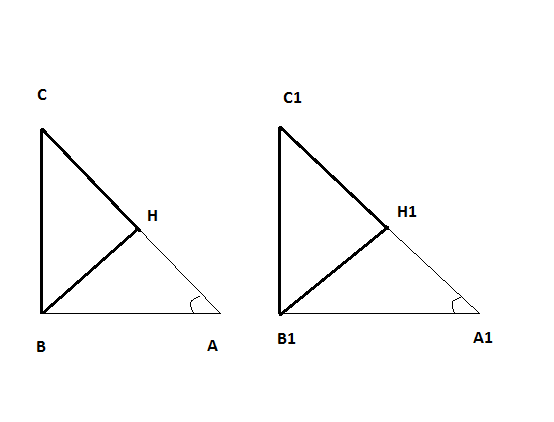
Даны  два  равных  прямоугольных  треугольника  АВС  и  А1В1С1, у которых  В = В1 =  90 градусов,  А =  А1; ВН и В1Н1 – высоты. Докажите, что ВНС =  В1Н1С1.

Answer 1

Поскольку треугольники АВС и А1В1С1 равны, то <C=<C1.Треугольники ВНС и В1Н1С1 - прямоугольные. У них:
ВС=В1С1 по условию, 
<C=<C1
Значит ВНС и В1Н1С1 равны, т.к. гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого.