Предмет: Алгебра,
автор: miass74rus
Найдите критические точки функции y=2x³-9 x²+7.
Определите, какие из них являются точками максимума, а какие - точками минимума.
Ответы
Автор ответа:
0
Для того, чтобы найти критические точки любой функции, для начала нужно найти её производную. Так и сделаем:

Далее приравниваем производную к нулю и решаем полученное уравнение. Тем самым мы найдём необходимые нам критические точки.

0 и 3 являются искомыми нами точками.
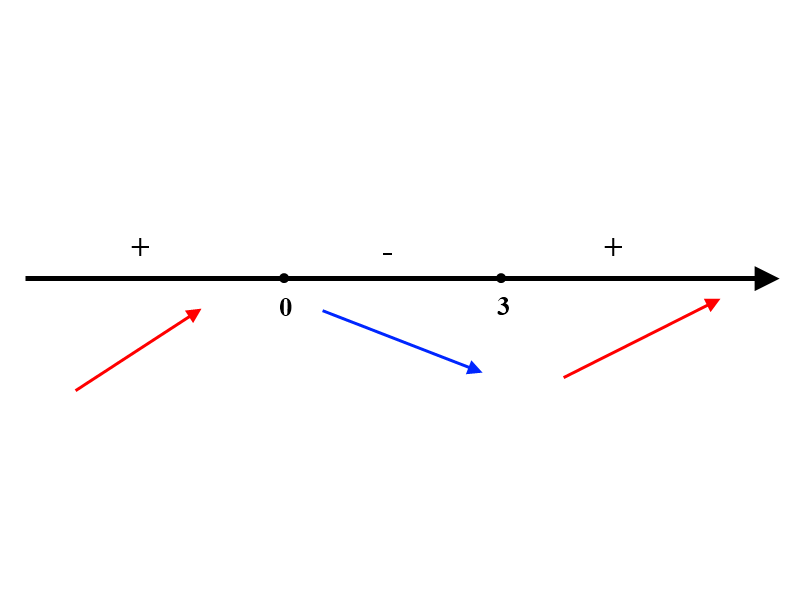
Строим координатную прямую, где располагаем наши точки для того, чтобы определить интервалы возрастания и убывания. Мы видим, что функция возрастает на промежутке (-бесконечность: 0), затем убывает на (0:3) и потом снова возрастает на (3:+бесконечность). Следовательно,

Далее приравниваем производную к нулю и решаем полученное уравнение. Тем самым мы найдём необходимые нам критические точки.
0 и 3 являются искомыми нами точками.
Строим координатную прямую, где располагаем наши точки для того, чтобы определить интервалы возрастания и убывания. Мы видим, что функция возрастает на промежутке (-бесконечность: 0), затем убывает на (0:3) и потом снова возрастает на (3:+бесконечность). Следовательно,
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Биология,
автор: tosikprivet3gmailcom
Предмет: Биология,
автор: kusainovi
Предмет: Математика,
автор: dsfadffadsg
Предмет: Литература,
автор: нурлубаева