Предмет: Алгебра,
автор: nastyaustyanceva
площадь треугольника ABC равна 120. найдите площадь треугольника CDE где D и E - середины сторон AC и CB соответственно. Скажите ответ.
Ответы
Автор ответа:
0
D и E - середины сторон AC и CB ,значит D Е- средняя линия Δ АВС и тогда ΔАВС подобен ΔС D Е по двум углам и коэффициент подобия ранен 1/2.
Площади подобных треугольников относятся как коэффициент подобия в квадрате, значит
S₁/S₂=(1/2)²
S₁- площадь ΔС D Е
S₂-площадь ΔАВС
S₁/120=1/4; S₁=120:4=30
Ответ :30
Площади подобных треугольников относятся как коэффициент подобия в квадрате, значит
S₁/S₂=(1/2)²
S₁- площадь ΔС D Е
S₂-площадь ΔАВС
S₁/120=1/4; S₁=120:4=30
Ответ :30
Автор ответа:
0
==========================
Приложения:
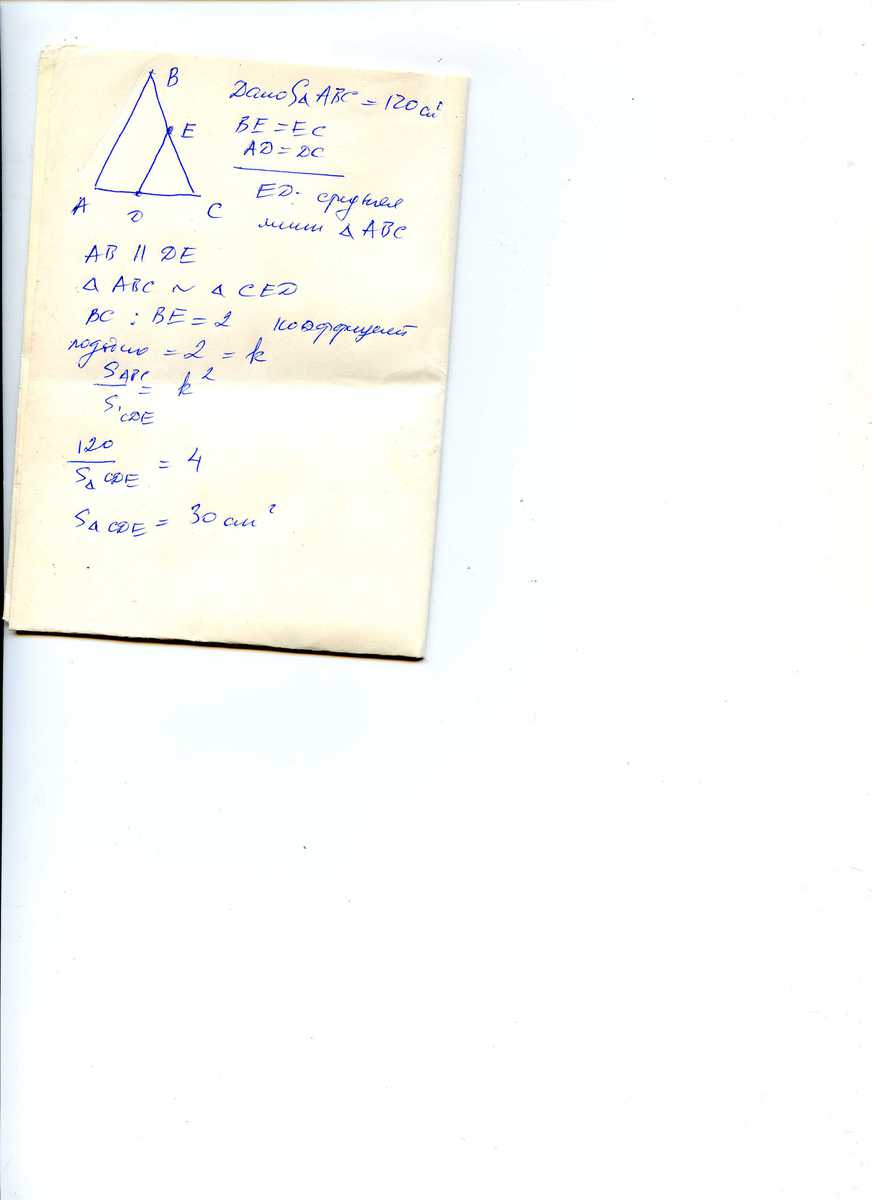
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: dajjxj
Предмет: История,
автор: texno240318
Предмет: Алгебра,
автор: alissa0699
Предмет: История,
автор: Nastia97228