Question

найдите точки экстремума заданной функции и определите их характер
y=5x^5-3x^3

Answer 1

$y=5x^5-3x^3 \ y`=25x^4-9x^2 \ y`=0 \ 25x^4-9x^2=0 \ x^2(x- frac{3}{5} )(x+ frac{3}{5} )=0$
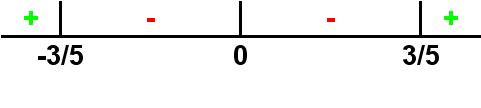
При переходе через точку -3/5 знак производной меняется с плюса на минус
При переходе через точку 3/5 знак производной меняется с минуса на плюс
Значит:
$x_{max}= -frac{3}{5} \ x_{min}= frac{3}{5}$

Answer 2

спасибо

Answer 3

$y=5x^{5}-3x^{3} D(f)=R (-infty;+-infty) y'=25x^{4}-9x^{2} y'=0 25x^{4}-9x^{2}=0 x^{2}=t 25t^{2}-9t=0 t*(25t-9)=0 t=0 25t-9=0 25t=9 t=9/25 t=0,36 x^{2}=0 x=0 x^{2}=0,36 x=+-0,6 x=0,6 (min) x=-o,6 (max)$  

Ноль это точка перехода.