Question

апофема правильной треугольной пирамиды равна 4, а высота пирамиды равна 2. найдите сторону основания пирамиды. должно получиться 12, не понимаю как.

Answer 1

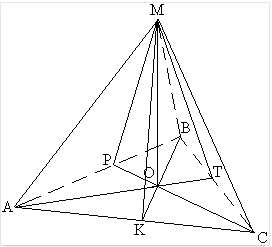
Дано: ОМ=2, МТ=4, ВС=АС=АВ
Найти: ВС
Решение:
Треугольник ОМТ прямоугольный. По т.Пифагора
ОТ²=МТ²-ОМ²=4²-2²=12
В правильном треугольнике СР является биссектриссой. Поэтому угол ОСТ равен половине угла АСВ, т.е. 60/2=30⁰.
Треугольник ОСТ прямоугольный. Гипотенуза в два раза больше катета, лежащего напротив угла в 30⁰. Следовательно, ОС=2ОТ=2√12
По т.Пифагора находим СТ²=ОС²-ОТ²=4*12-12=36
СТ=6
ВС=2СТ=2*6=12
Ответ: 12