Question

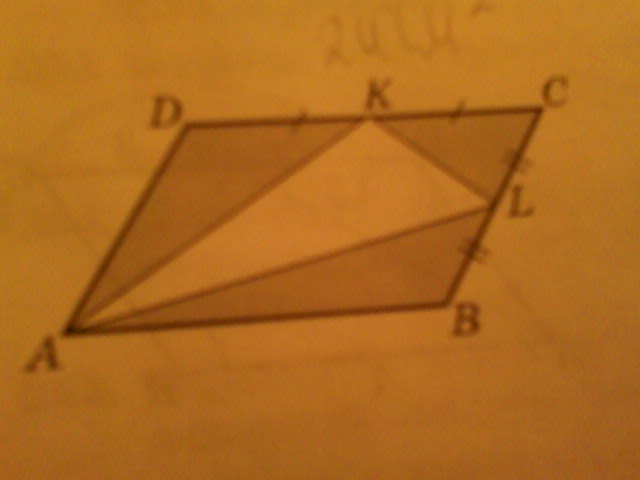
abcd параллелограмм s abcd=24 см^2. DK=KC BL=LC.
Найдите площадь треуг.AKL

Answer 1

параллелограмм АДСВ площадью=24, ДК=КС, СЛ=ЛВ, проводим диагонали АС и ДВ, диагональ АС делит параллелограмм на 2 равных треугольника, площадь АДС=площадьАВ=1/2площадьАДСВ=24/2=12, треугольник АДС, АК-медиана и делит треугольник на 2 равновеликих треугольника, площадьАДК=площадьАКС=1/2площадь АДС=12/2=6, треугольник АСВ, АЛ-медиана, площадь АСЛ=площадь АЛВ=1/2площадь АСВ=12/2=6, 
площадь АКСЛ=площадьАКС=площадьАСЛ=6+6=12, 
треугольник ДСВ площадью1/2АДСВ=24/2=12, КЛ-средняя линия треугольника параллельна ДВ=1/2ДВ, СН-высота на   ДВ, площадь ДСВ=1/2*ДВ*СН=12, средняя линия КЛ делит высоту на 2 равные части=1/2СН, тогда площадь КСЛ=1/2*КЛ*1/2СН=1/2*1/2ДВ*1/2СН=1/8ДВ*СН, т.е площадьКСЛ=площадьДВС*2/8=12*2/8=3, 
площадьАКЛ=площадьАКСЛ-площадьКСЛ=12-3=9