Question

Окружность,построенная на стороне AC треугольник ABC как на диаметре,проходит через середину стороны BC и пересекает в точке D продолжение стороны AB за точку А, причем AD=(2/3)AB. найти площадь треугольника ABC, если АС=1

Answer 1

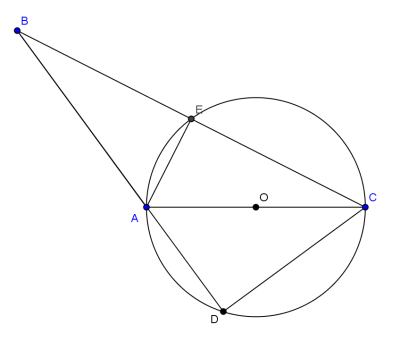
Окружность, построенная на стороне `AC` треугольника `ABC` как на диаметре, проходит через середину стороны `BC` и пересекает в точке  `D` продолжение стороны `AB` за точку `A` причём `AD=2/3*AB`. Найдите площадь треугольника `ABC`, если `AC= 1`. Угол `AEC` - прямой, так как он опирается на диаметр. Кроме того, по условию `BE=EC`. Отсюда `AB=AC=1`. Поскольку `AD=2/3*AB`, то `AD=2/3`. По теореме Пифагора находим `DC`. Площадь треугольника `ABC` равна `1/2*AB*CD=sqrt(5)/6` Ответ: `sqrt(5)/6`