Question

Помогите пожалуйста.

1 вариант

1. Дан треугольник АВС. Постройте точку, симметричную точке А относительно прямой ВС.

2. Посторойте точку М1, симметричную точке М(4;-3) относительно начала координат. Запишите координаты построенной точки.

3. Найдите периметр прямоугольного треугольника с гипотенузой 12 см и радиусом вписанной окружности 3 см.

 

2 вариант.

1. Дан треугольник АВС. Постройте точку А1, симметричную А относительно вершины С.

2. Постройте точку D1, симметричную точке D(-3;2) относительно оси ОХ. Запишите координаты построенной точки.

3. Центральный угол АОВ на 50 градусов больше вписанного в окружность угла АСВ, опирающегося на дугу АВ. НАйти углы АОВ и АСВ.

Желательно с объяснениями. Заранее спасибо.

 

Answer 1

Вариант 1.

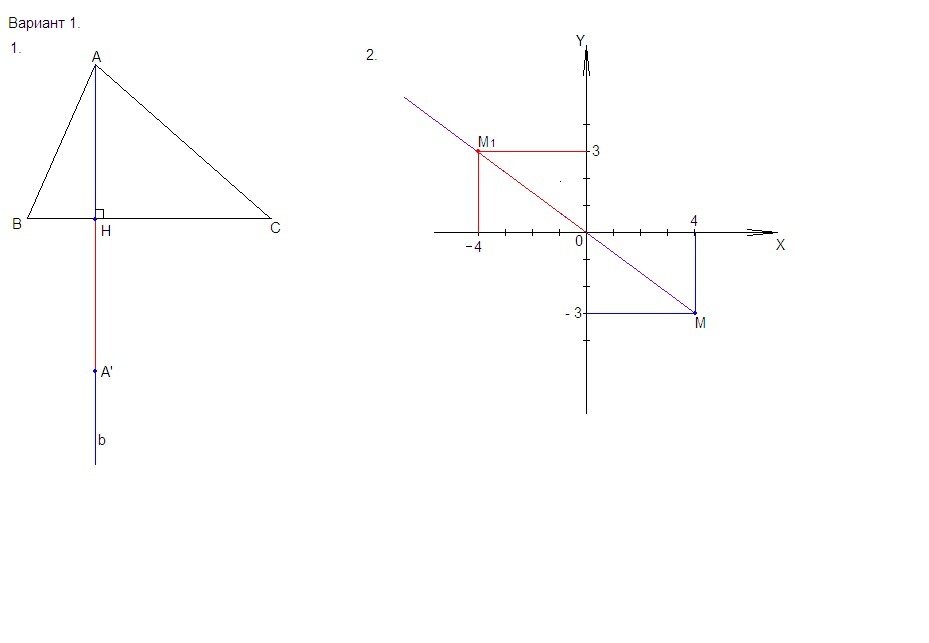
1. Проводим луч b с началом в точке А перпендикулярно прямой ВС.
b∩BC = H.
На луче b по другую сторону от прямой ВС откладываем отрезок НА' = AH.
Точка A' построена.

2. Проводим луч МО. На этом луче за точку О откладываем отрезок ОМ₁= МО. Точка М₁ построена. М₁(- 4 ; 3)

3. Обозначим  гипотенузу с, r - радиус вписанной окружности.
Для прямоугольного треугольника справедлива формула:
r = p - c, где р - его полупериметр.
p = r + c = 3 + 12 = 15 см

Вариант 2.

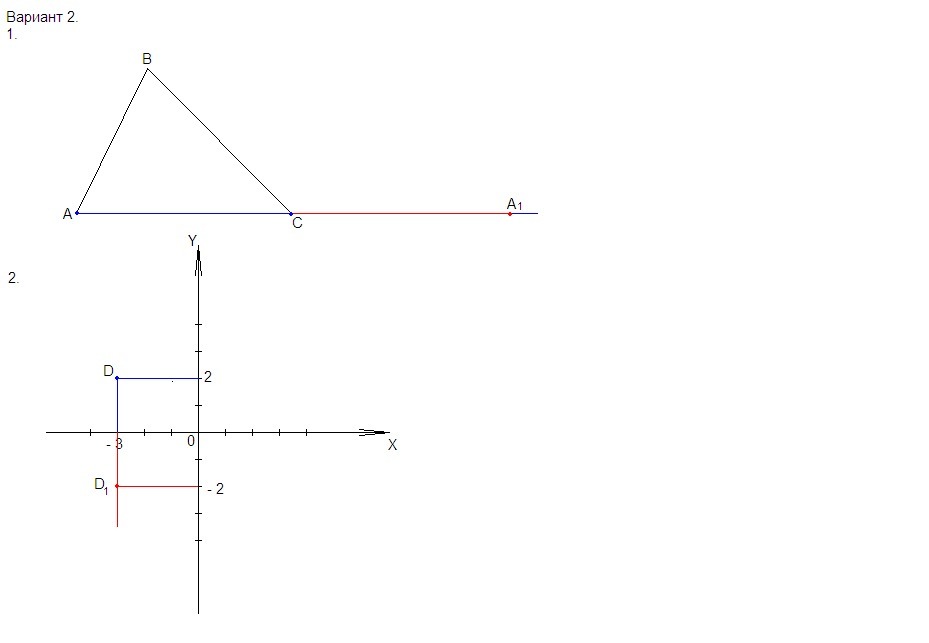
1. Проводим луч АС. На этом луче за точку С откладываем отрезок СА₁= АС. Точка А₁ построена.

2. Проводим луч с началом в точке D, перпендикулярно оси Ох. Пусть он пересечет ос Ох в точке Н. На это луче за точку Н откладываем отрезок HD₁ = DH. Точка D₁ построена. D₁(- 3 ; - 2).

3. Центральный угол в два раза больше вписанного, опирающегося на ту же дугу.
Пусть вписанный ∠АСВ = х, тогда ∠АОВ = 2х.
2x - x = 50
x = 50
∠АСВ = 50°
∠АОВ = 100°