Предмет: Геометрия,
автор: twilightbella
Докажите, что медианы треугольника разбивают его на шесть равновеликих треугольников.
Ответы
Автор ответа:
0
Пусть Sabc = S
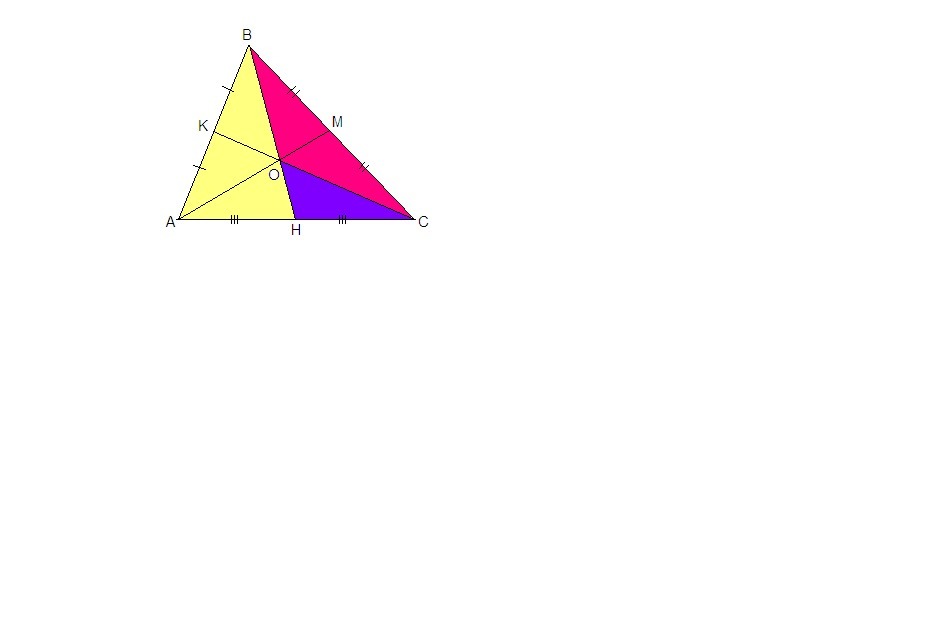
Медиана ВН делит треугольник АВС на два равновеликих.
Значит, Sabh = Scbh = S/2.
Треугольники СОН и СОВ имеют общую высоту, проведенную из вершины С, поэтому их площади относятся, как основания, к которым проведена высота.
Т.е.
Scoh/Scob = OH/OB = 1/2 (т.к. медианы точкой пересечения делятся в отношении 2:1, считая от вершины)
Т.е. Scoh = Scob/2 = Schb/3 = S/6
Аналогично доказывается, что каждый из образовавшихся треугольников имеет площадь S/6.
Медиана ВН делит треугольник АВС на два равновеликих.
Значит, Sabh = Scbh = S/2.
Треугольники СОН и СОВ имеют общую высоту, проведенную из вершины С, поэтому их площади относятся, как основания, к которым проведена высота.
Т.е.
Scoh/Scob = OH/OB = 1/2 (т.к. медианы точкой пересечения делятся в отношении 2:1, считая от вершины)
Т.е. Scoh = Scob/2 = Schb/3 = S/6
Аналогично доказывается, что каждый из образовавшихся треугольников имеет площадь S/6.
Приложения:
Автор ответа:
0
разве СО высота?
Автор ответа:
0
На рисунке высота не проведена, но если ее провести из вершины С к прямой ВН, то она будет высотой и для треугольника СОН и для СОВ.
Похожие вопросы
Предмет: Информатика,
автор: aruzhankapparbek
Предмет: Геометрия,
автор: Аноним
Предмет: Алгебра,
автор: Dauletew
Предмет: Химия,
автор: морковка1