Question

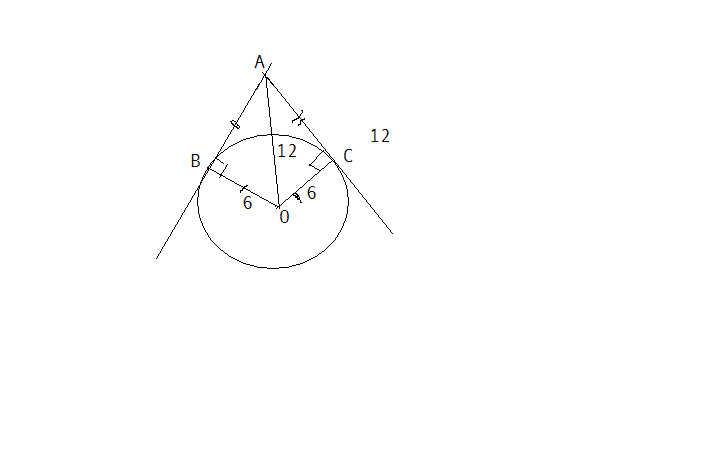
АВ и АС касательные к окружности с центром О.ВО=6см, АО=12 см. Найдите угол между касательными.

 

Answer 1

Рисунок прикреплю позже

Треугольник ОВА прямоугольный с прямым углом В( так как радиус перпендикулярен касатеотной в, проведённый в точку касания)

 в этом треугольнике ОВ=6см ОА=12 см( по условию) ОА также и гипотенуза. Катет который равен половине гипотенузы лежит напротив угла в 30 градусов, т.е ВО =1/2Ао следовательно противолежащий катету ВО угол ВАО равен 30 градусов. Так как треугольники ОВА и ОСА равны по ттретьему признаку(ОВ=ОС, ОА общая, АВ=АС по свойству касательных) то углы ВАО и САО также равны. Поэтому искомый угол равен 60 градусов

 Ответ 60