Question

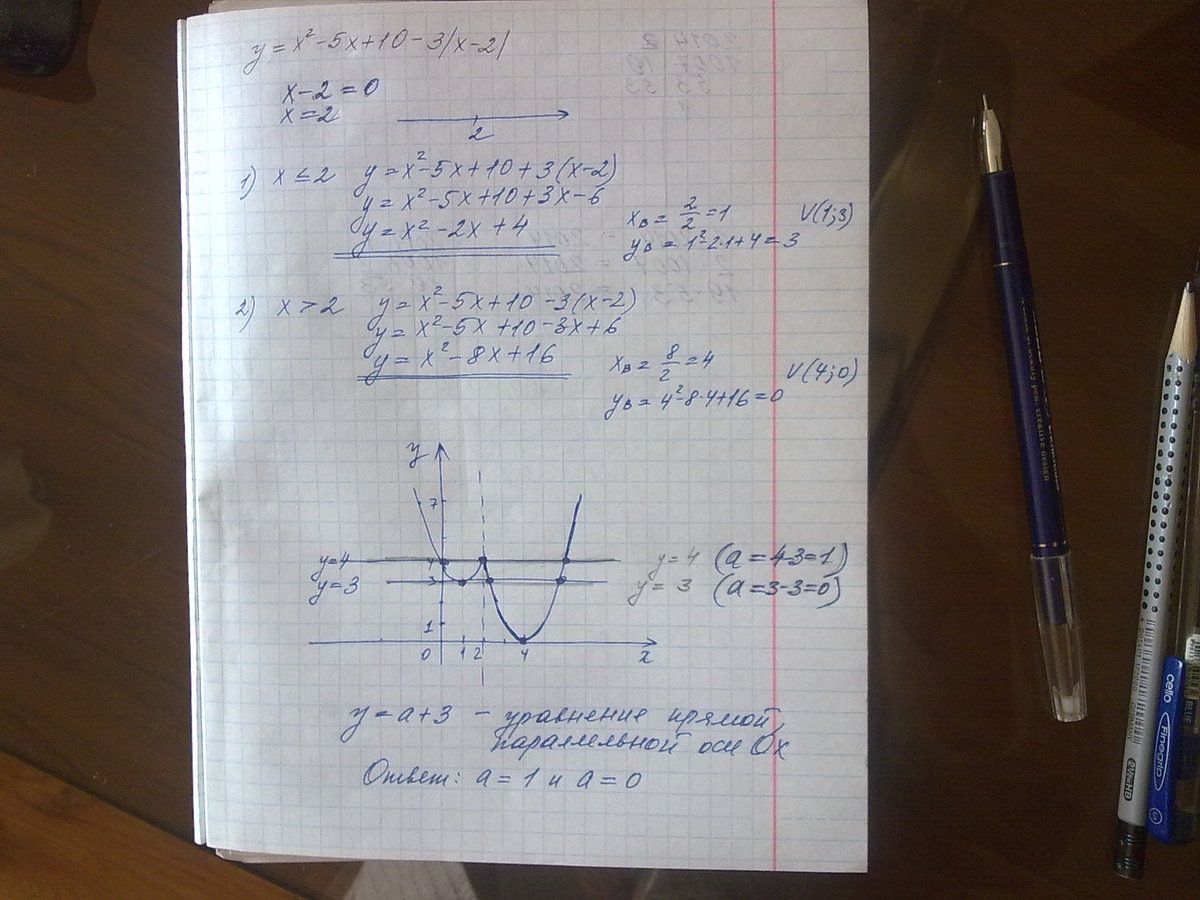
помогите решииить, пожааалуйста! Постройте график функции y=x^2-5x+10-3|x-2| и определите при каких значениях а, график имеет ровно три общие точки с прямой y=a+3.

Answer 1

Начнём с того, что график функции представленный на рисунках не соответствует функции заданной в виде формулы: y=(x-1)/(x^2 - x). Поэтому считаем что формула верна и делаем небольшое элементарное её преобразование, то есть в числителе х выносим за скобку и получаем: y=(x-1)/(x*(x-1)) => y=1/x. График этой функции представлен на моём рисунке фиолетовым цветом: ветвь обозначенная цифрой 1 при х>0, а цифрой 2 при х<0.  

Как выглядит функция у=kx читайте выше у Светланы Кузнецовой. На моём рисунке эта функция показана коричневыми прямыми выходящими из начала координат для 6 разных коэффициентов k: 

1) при k от 0 до 1 (ни 0 ни 1 не входят); 
2) при k = 1; 
3 при k > 1; 
4) при k от -1 до 0 (ни -1 ни 0 не входят); 
5) при k = -1; 
6) при k < -1; 

Хочу заметить что коричневые прямые на самом деле не заканчиваются в начале координат и должны быть продолжены вниз (с начало не заметил а потом уже не было времени исправлять) 

Глядя на рисунок хорошо видно, что график функции y=kx пересекает график функции y=1/x (то есть имеет 1 общую точку) при любом k кроме случая когда k=0. 

Answer 2

..................................

Answer 3

почему из 4 надо вычитать 3, и из 3 вычитать 3?

Answer 4

у=а+3 и имеется прямая у=4 => а+3=4, а=4-3=1. Аналогично, у=а+3 и имеем прямую у=3 => a+3=3, a=3-3=0