Предмет: Алгебра,
автор: Pringles657
Найдите площадь фигуры, ограниченной линиями:

Ответы
Автор ответа:
0
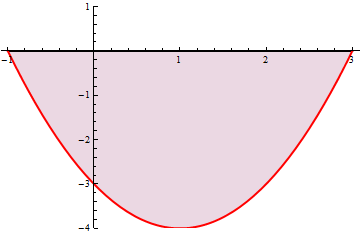
Сначала нужно найти те точки, где эти линии пересекаются (т.е. значения равны). Это можно сделать, решив уравнение  , но я построил график.
, но я построил график.
Теперь вспомним смысл интеграла - интеграл от a до b от функции f(x) равен площади под графиком функции.
Главный вопрос тут - чему равны a и b? Да это ж те самые корни уравнения! Мы интегрируем от а до b - значит мы находим площадь под графиком от x=a до x=b.

Ответ: -32/3
Теперь вспомним смысл интеграла - интеграл от a до b от функции f(x) равен площади под графиком функции.
Главный вопрос тут - чему равны a и b? Да это ж те самые корни уравнения! Мы интегрируем от а до b - значит мы находим площадь под графиком от x=a до x=b.
Ответ: -32/3
Приложения:
Автор ответа:
0
Это понятно, только площадь отрицательной быть не может! Но Все равно спасибо)
Автор ответа:
0
По сути просто поменять знак.
Похожие вопросы
Предмет: Информатика,
автор: vksaharkov
Предмет: Информатика,
автор: vladimir26997
Предмет: Математика,
автор: ulyanayano
Предмет: Химия,
автор: yra1997goda