Question

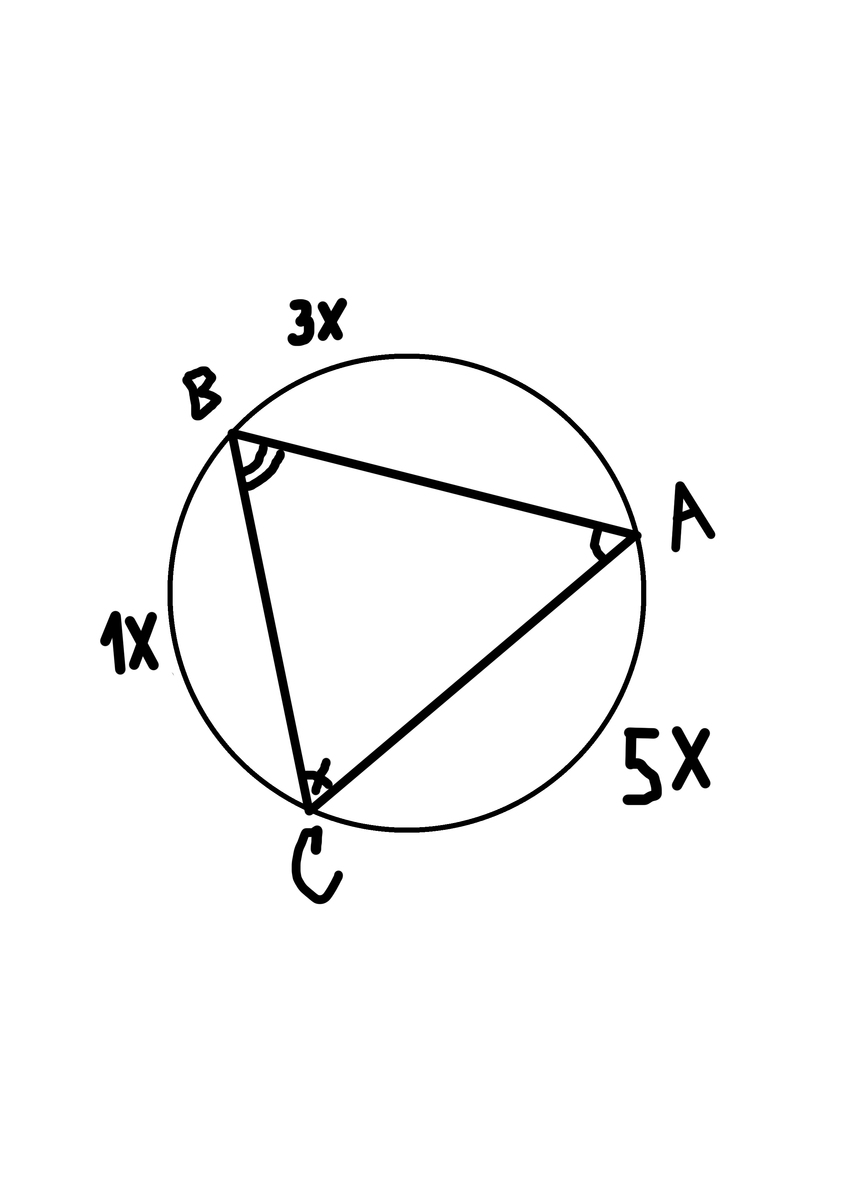
1. Вершины треугольника ABC делят окружность в отношении 1:3:5. Найдите углы этого треугольника.
2. Радиус окружности равен 10 см, а расстояние от одного конца диаметра до точки окружности - 16 см. Найдите расстояние от другого конца диаметра до этой точки.

Answer 1

1.вписанный угол = 1/2 дуги на которую он опирается. Пусть  дуга АС=5х, ВС= х, АВ=3х.Тогда уголАВС=1/2 *5х,ВАС=1/2х,АСВ=1/2*3х. тогда 
АВС+ВАС+АСВ=180;
1/2*5х+1/2*х+1/2*3х=180
1/2*9х=1804.5х=180
х=40
АВС=100
ВАС=20
АСВ=60
2.r = 10, d = 20 см, угол С = 90, АС = 16 см.
 По теореме Пифагора 
с2 = а2 + в2 
Отсюда
 а2 = с2-в2
а=корень( с-в)
ВС= 2 см