Question

в правильной треугольной пирамиде сторона основания равна 3 см, а боковые ребра наклонены к плоскости основания под углом 60 градусов. найдите радиус описанной вокруг пирамиды сферы

Answer 1

Решение:
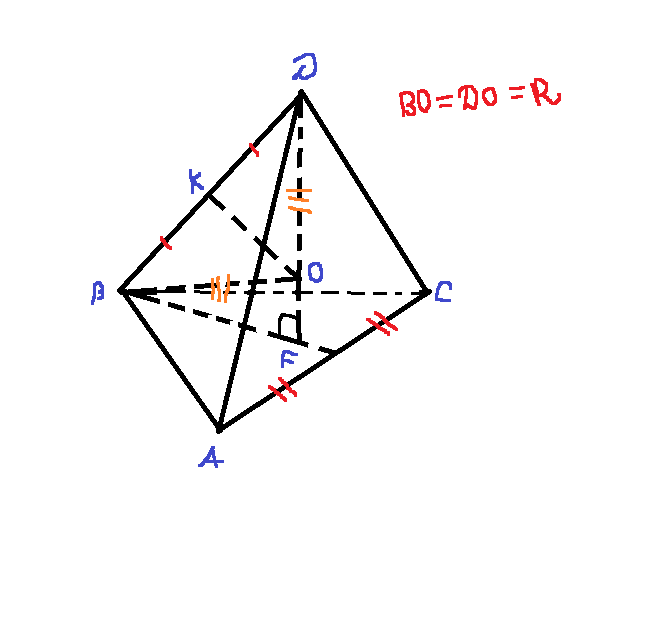
ВF=R1
R1-радиус описанной окружности основания
R1=√3a/3
R1=√3*3/3=√3=BF
Рассмотрим треугольник BDF. 
угол DBF = 60 (По условию)
Значит угол BDF равен 30⇒
⇒BD=2√3
DF²=(2√3)²-(√3)²=3²
DF=3
Треугольник BDF подобен треугольнику OKD
по двум углам.
BF/DF=KO/KD
√3/3=KO/√3
KO=1
DO²=KD²+KO²=(√3)²+1²=4
DO=BO=R=2
Ответ:R=2

Answer 2

Проверь