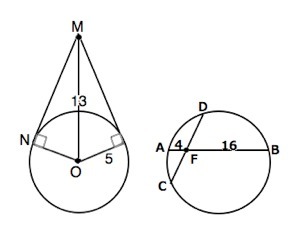
1) МN и MK - отрезки касательных, проведенных к окружности радиусом 5 см. Найдите MN и MK, если МО = 13 см.
2) Хорды АВ и CD пересекаются в точке F так, что AF= 4 см, BF = 16 см, СF =DF. Найти СD
Ответы
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. (теорема).
В ∆ ОMN и ∆ ОMK углы при вершине М равны, MN=MK, МО - общая, ОМ=ОК. ⇒ ∆ ОMN = ∆ ОMK
Радиус, проведенный в точку касания, перпендикулярен касательной.
∆ ОMN и ∆ ОMK - прямоугольные. Если не помните, что при отношении катета к гипотенузе 5:13 второй катет равен 12, можно MN и MK найти по т.Пифагора.
MN=√(MO²-ON²)=√144=12 см– это ответ.
* * *
Если две хорды окружности пересекаются в некоторой точке, то произведение отрезков одной хорды равно произведению отрезков другой хорды. (теорема).⇒
АF•BF=CF•DF
Так как по условию CF=DF, то
CF²=4•16=64
CF=√64=8 см
CD=2CF=16 см