Предмет: Алгебра,
автор: ulbosik
Пожалуйста помогите! Заранее спасибо)
Приложения:
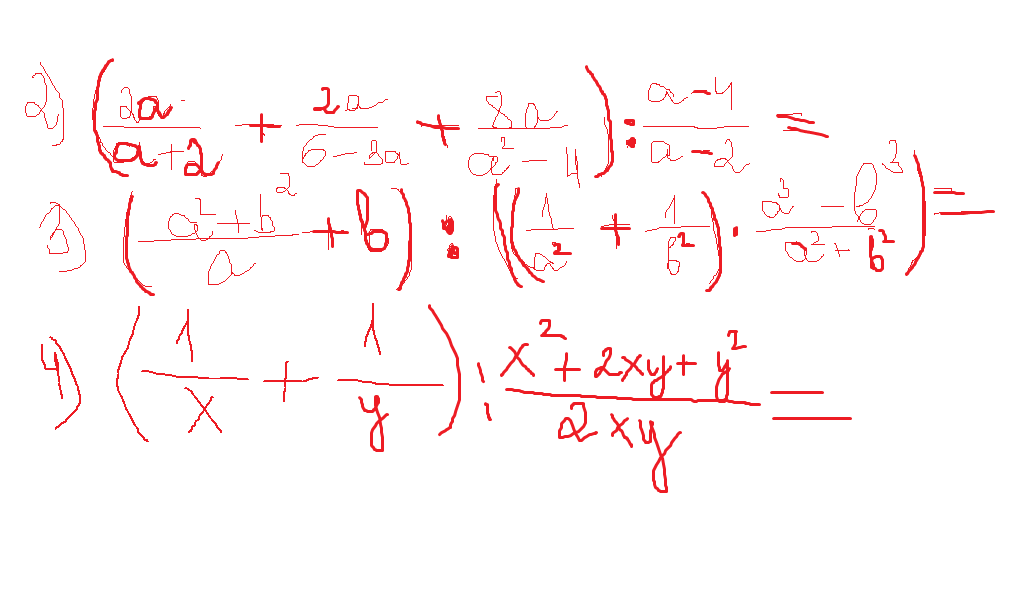
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: География,
автор: kolanovna2000
Предмет: Химия,
автор: abricocik
Предмет: Математика,
автор: kasymsahizada
Предмет: География,
автор: aigulkaasbaganova
Предмет: Математика,
автор: vikajunya