Question

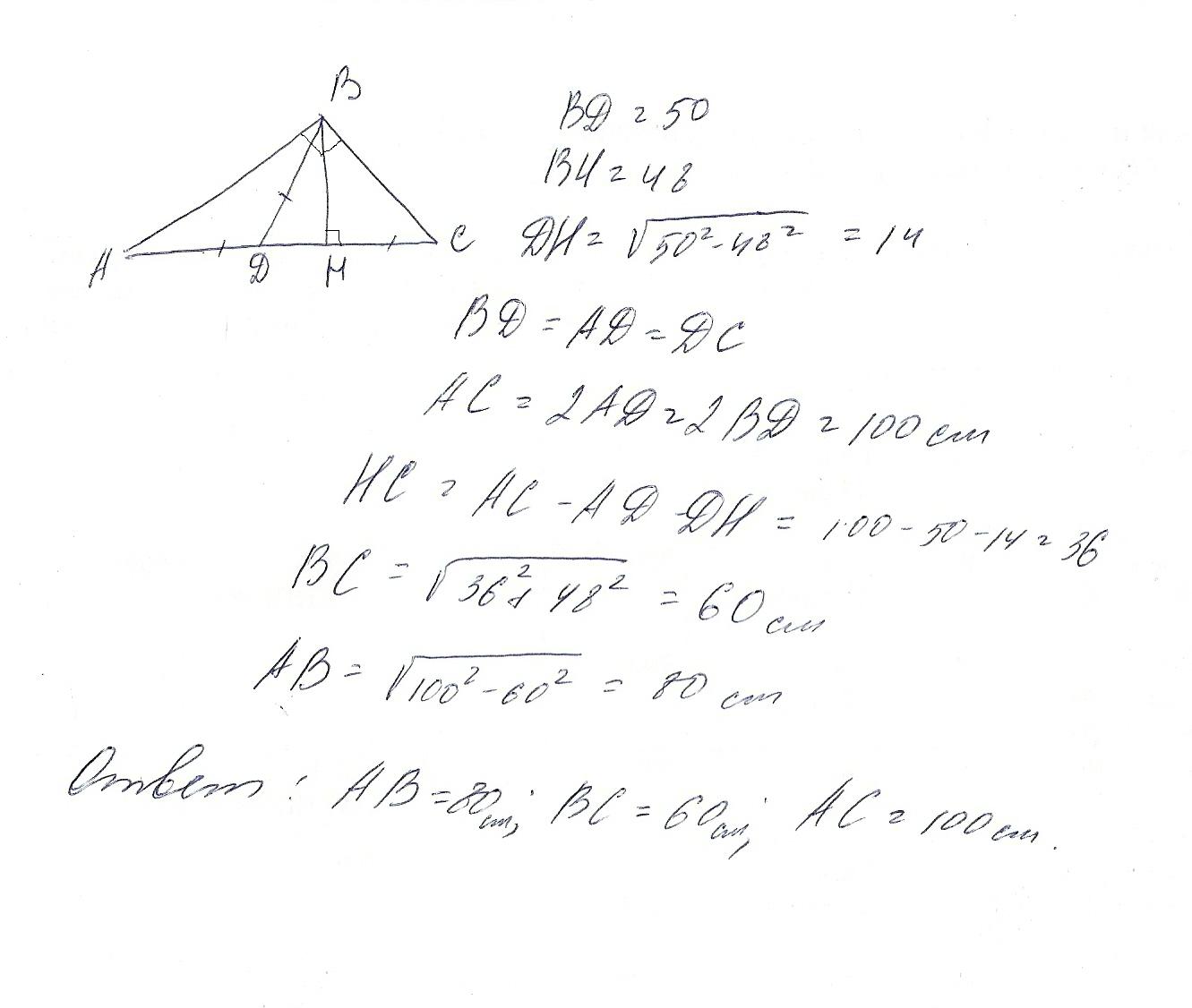
Медиана и высота прямоугольниго треугольника проведённые к гипотенузе равны 50см и 48см. Найдите стороны треугольника.

Answer 1

(смотри в вложениях).......

Answer 2

Основание точки высоты обозначим за H. Основание точки медианы обозначим точкой M. Медиана у прямогугольного треугольника выпущеная из прямого угла является радиусом описаной окружности прямоугольного треугольника. Точка M  является центром описанной окружности. Значит BM = MA = MC. 

Значит гипотенуза = 50 + 50 = 100 см.

Треугольник MBH - прямоугольный => MH^2 = 50^2 - 48^2 => MH = 14cм.

Треугльник ABH - прямоугольный => AB^2 = 48^2 + (50 + 14)^2 => AB = 80 см.

Из прямоугольного треугольника CHB находим BC^2 = (50 - 14)^2 + 48^2 => BC = 60 см.

Ответ: AC=100cm  AB=80cm  BC = 60cm