Предмет: Алгебра,
автор: Astroz
Помогите решить, никак не могу понять что делать дальше, нашёл производную а дальше какая то фигня получается
Приложения:
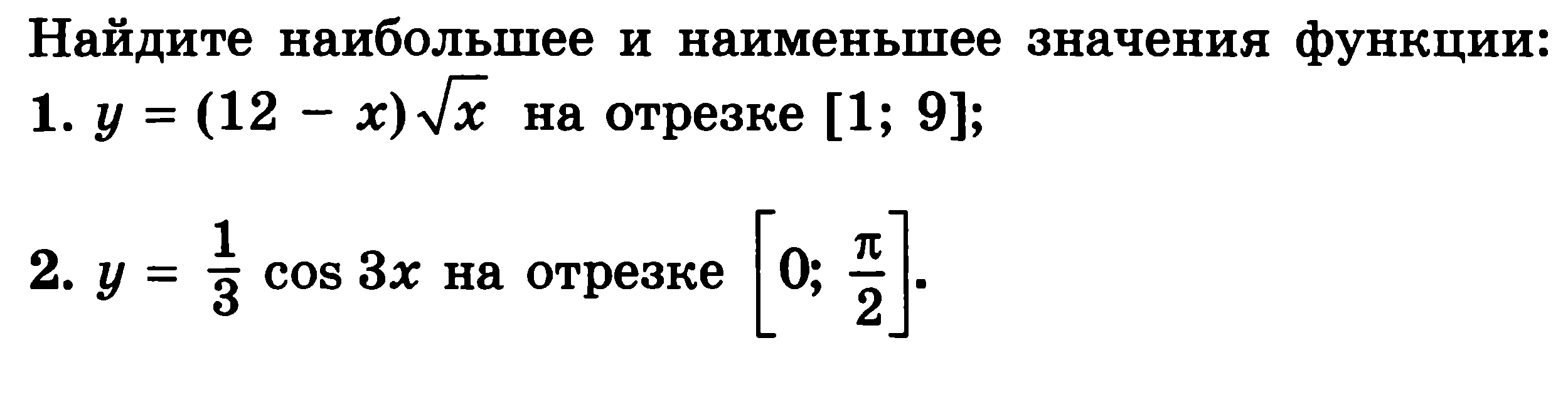
Ответы
Автор ответа:
0
1. Делаем замену t = √x, t ∈ [1, 3]
u(t) = y(x(t)) = (12 - t^2) t = 12t - t^3
u'(t) = 12 - 3t^2 = 12(4 - t^2) = 0
t^2 - 4 = 0
t = 2 (второй корень не в промежутке)
Проверяем значения на концах и там, где производная обращается в ноль:
t = 1: u(1) = 12 - 1 = 11
t = 2: u(2) = 24 - 8 = 16
t = 3: u(3) = 36 - 27 = 9
Минимальное значение 9, максимальное 16
2. y' = 1/3 * (-sin 3x) * 3 = -sin 3x = 0
x = 0, x = π/3
Значения:
y(0) = 1/3
y(π/3) = -1/3
y(π/2) = 0
Минимальное значение -1/3, максимальное 1/3
u(t) = y(x(t)) = (12 - t^2) t = 12t - t^3
u'(t) = 12 - 3t^2 = 12(4 - t^2) = 0
t^2 - 4 = 0
t = 2 (второй корень не в промежутке)
Проверяем значения на концах и там, где производная обращается в ноль:
t = 1: u(1) = 12 - 1 = 11
t = 2: u(2) = 24 - 8 = 16
t = 3: u(3) = 36 - 27 = 9
Минимальное значение 9, максимальное 16
2. y' = 1/3 * (-sin 3x) * 3 = -sin 3x = 0
x = 0, x = π/3
Значения:
y(0) = 1/3
y(π/3) = -1/3
y(π/2) = 0
Минимальное значение -1/3, максимальное 1/3
Похожие вопросы
Предмет: Қазақ тiлi,
автор: sobiramahsutova
Предмет: Другие предметы,
автор: alishersabitov090
Предмет: Информатика,
автор: artiishhh
Предмет: Математика,
автор: cdtnf16