Предмет: Алгебра,
автор: ксениz
упростите выражение 1 и 3 пожалуйста
Приложения:
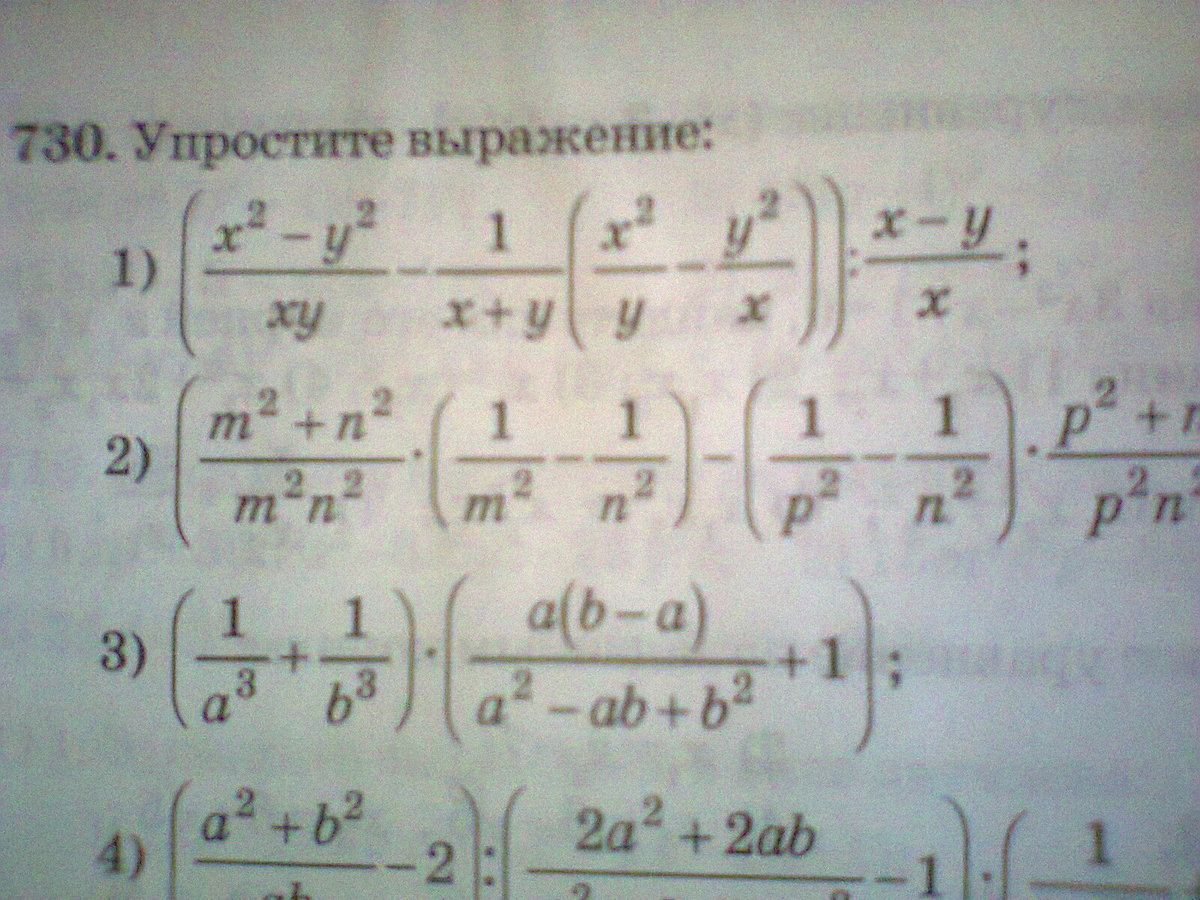
Ответы
Автор ответа:
0
1)

3)

3)
Автор ответа:
0
что это?
Автор ответа:
0
решение 1 и 3
Автор ответа:
0
спасибо
Похожие вопросы
Предмет: Математика,
автор: cjbstprp
Предмет: Геометрия,
автор: oliviababanina
Предмет: Английский язык,
автор: xkyznezsovka
Предмет: Алгебра,
автор: ДиашкаLove
Предмет: Математика,
автор: serovamv