Предмет: Алгебра,
автор: Аноним
тОЛЬКО ПОД БУКВОЙ А!!!!!!!!!!!!!!!1
Приложения:
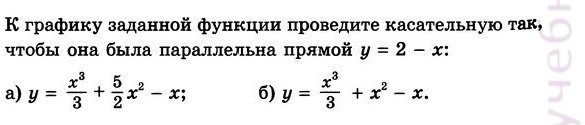
Ответы
Автор ответа:
0
Y = f(a) + f '(a)*(x - a) - уравнение касательной
f(a) = (a^3)/3 + 2.5a^2 - a
f '(a) = a^2 + 5a - 1
Y = (a^3)/3 + 2.5a^2 - a + (a^2 + 5a - 1)(x - a) = (a^2 + 5a - 1)*x + ((a^3)/3 + 2.5a^2 - a - a^3 - 5a^2 + a) = (a^2 + 5a - 1)*x - ((2a^3)/3 + (5a^2)/2)
Y || (2 - x) - у них должен быть одинаковый коэффициент перед х (k= -1)
a^2 + 5a - 1 = -1
a*(a + 5) = 0
a=0, a= -5
Если а=0: Y = -x
Если а= -5: Y = -x - 125/2
f(a) = (a^3)/3 + 2.5a^2 - a
f '(a) = a^2 + 5a - 1
Y = (a^3)/3 + 2.5a^2 - a + (a^2 + 5a - 1)(x - a) = (a^2 + 5a - 1)*x + ((a^3)/3 + 2.5a^2 - a - a^3 - 5a^2 + a) = (a^2 + 5a - 1)*x - ((2a^3)/3 + (5a^2)/2)
Y || (2 - x) - у них должен быть одинаковый коэффициент перед х (k= -1)
a^2 + 5a - 1 = -1
a*(a + 5) = 0
a=0, a= -5
Если а=0: Y = -x
Если а= -5: Y = -x - 125/2
Похожие вопросы
Предмет: Музыка,
автор: Аноним
Предмет: История,
автор: alesya246
Предмет: Биология,
автор: kirillgagra555
Предмет: Математика,
автор: Niuta201