Предмет: Алгебра,
автор: Аноним
РАЗЛОЖИТЕ МНОГОЧЛЕНЫ НА МНОЖИТЕЛИ.
Решите, пожалуйста, примеры с номера 30.24-28 (А;Б)
Спасибо.
Приложения:
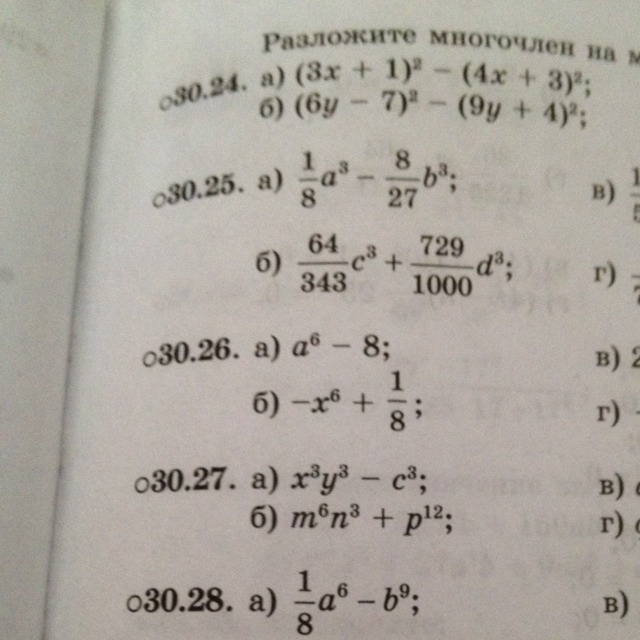
Ответы
Автор ответа:
0
30.24
используем формулу разности квадратов
а)

б)

30.25
используем формулу разности и суммы кубов

а)

б)

30.26 используем формулу разности и суммы кубов

и формулу
а)
б)
30.27 используем формулу разности и суммы кубов

и формулы
а)
б)
30.28
а)
используем формулу разности квадратов
а)
б)
30.25
используем формулу разности и суммы кубов
а)
б)
30.26 используем формулу разности и суммы кубов
и формулу
а)
б)
30.27 используем формулу разности и суммы кубов
и формулы
а)
б)
30.28
а)
Похожие вопросы
Предмет: Русский язык,
автор: gemer333
Предмет: Алгебра,
автор: promv2224
Предмет: Математика,
автор: Zozuly9999
Предмет: Химия,
автор: meryjeff