Question

Определите промежутки монотонности функции:
a) y=3x^2 - 6x + 1
б) y=x^9 - 9x

Answer 1

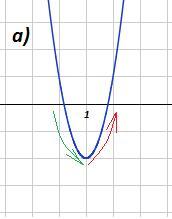
a) y = 3x² - 6x + 1   -  квадратичная функция, график - парабола, ветви направлены вверх ( а = 3 > 0).  Промежутки монотонности отделяются координатой х вершины параболы.

$x_o=-dfrac b{2a}=-dfrac{-6}{6}=1$

x∈ (-∞; 1] - функция убывает

x∈ [1; +∞) - функция  возрастает

---------------------------------------------------------------------

б) y = x⁹ - 9x

Для нахождения промежутков монотонности нужно найти экстремумы функции с помощью первой производной.

y' = (x⁹)' - (9x)' = 9x⁸ - 9 = 9(x⁸ - 1)

9(x⁸ - 1) = 0;    ⇒    x⁸ = 1;    ⇒     x₁ = 1; x₂ = -1

Интервалы знакопостоянства для производной функции y'

+++++++++ [-1] ------------ [1] +++++++++> x

        /                                       /

x∈ (-∞; -1] ∪ [1; +∞)  -  функция возрастает

x∈ [-1; 1]  -  функция убывает