Помогите пожалуйста! Срочно нужно..
Решите систему неравенств:
| log₂ (49 - x²) ≤ 2 + log₂ (x + 1)
<
| log₀.₄ (2|x - 3|+|x - 8|- 8) < 1
Ответы
log₂ (49 - x²) ≤ 2 + log₂ (x + 1)
ОДЗ: 49-x^2 >0; x+1>0
log₂ (49 - x²) ≤ log₂ 4 + log₂ (x + 1)
log₂ (49 - x²) ≤log₂ 4*(x+1)
log₂ (49 - x²) - log₂ 4*(x+1) ≤0
log₂ (49 - x²)/(4x+4) ≤0
log₂ (49 - x²)/(4x+4)≤log₂1
(49 - x²)/(4x+4)≤ 1
ну это уже можете дорешать сами
это решение первого неравенства,а второе вприцинпе логарифмируйте правую часть,и раскрывайте модули(получится 4случая)((
1) ОДЗ: (49 - x²) >0; x>-1
(x-7)(x+7)<0
log₂ (49 - x²) ≤ log₂4 + log₂ (x + 1);
log₂ (49 - x²)-log₂ (4x + 4) ≤ 0;
(По теореме):(2-1)(49- x²-4x-4)≤0;
x²+4x-45≤0;
x1=5; x2=-9;
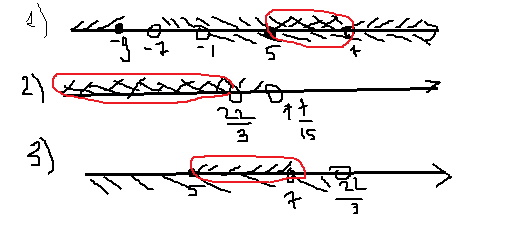
Решение 1-го: [5;7) т.к. решение положительно, то во 2-м модули просто убираются!
2) log₀.₄ (3x - 22) < 1(log₀.₄ 0.4); ОДЗ: (3x-22)>0; x>22/3
3x-22<0.4
x<112/15(7⁷/₁₅)
Решение 2-го: (-бесконеч.;22/3)
общее решение: [5;7)