Question

Длина окружности, описанной вокруг равнобедренного треугольника, равна 50Псм. Найти периметр треугольника если высота, проведенная к основанию, равна 32 см.

Answer 1

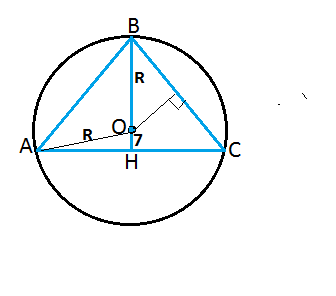
Обозначим вершины треугольника АВС, основание высоты - Н. 
Длина окружности =2 π r
2 п r=50 π 
Коротко запись задачи выглядит так:
r=50п:2п=25
32-25=7
Р= 2√(25²-7²)+2√(32²+24²)=128см
Подробно: 
Высота равнобедренного треугольника - срединный перпендикуляр. 
Центр описанной окружности треугольника лежит на пересечении срединных перпендикуляров. Так как радиус меньше высоты треугольника, центр лежит на этой высоте. Обозначим центр О.
Расстояние от вершины треугольника В до центра окружности О равно R
Расстояние ОН от центра окружности до середины основания треугольника АВС
32-25=7 см
Соединим центр О с вершиной угла основания. Получим треугольник АОН.
АО= радиусу и равна 25 см 
Найдем половину основания по формуле Пифагора из треугольника АОН
АН=√(25²-7²)=24 см
Основание треугольникаАС равно 2*24=48см
Из треугольника АВН найдем боковую сторону треугольника АВ
АВ=√(32²+24²)=40смВС=АВ=40 см
Периметр Δ АВС
Р=2·40+48=128 см