Предмет: Геометрия,
автор: Аноним
Докажите, что если одна сторона прямоугльгика равна стороне треугольника, а вторая сторона - половине высоты, опущенной на эту сторону треугольника, то площади прямоугольника и треугольника будут равны. Решение с рисунком, пожалуйста, очень надо.
Ответы
Автор ответа:
0
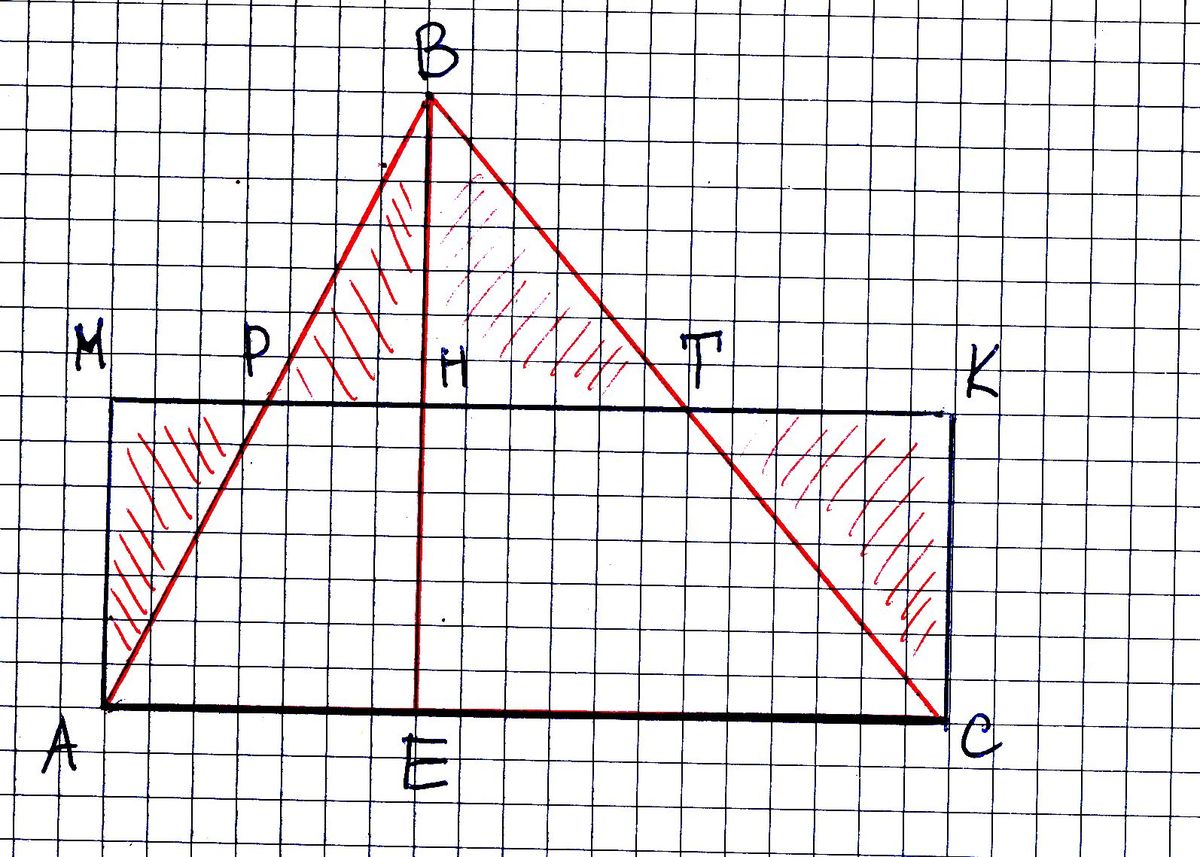
На четреже дано ГЕОМЕТРИЧЕСКОЕ решение задачи. На общем основании АС построены прямоугольник АМКС и треугольник АВС. ВЕ - высота треугольника, равна 2*МН.
Легко доказать равенство треугольников АМР и РНВ, и треугольников ВНТ и ТКС.
Действительно, МА = ВН = ВЕ/2, а углы при соотвествующих сторонах равны, как накрест лежащие при параллельных и секущей (ВЕ II MA и ВЕ II KC, это все перпендикуляры к АС).
Поэтому площадь треугольника равна площади прямоугольника.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: morvak38
Предмет: Алгебра,
автор: tikitoki30
Предмет: Русский язык,
автор: VannyFnaF
Предмет: Биология,
автор: мороженное
Предмет: Физика,
автор: M51Kseries