Question

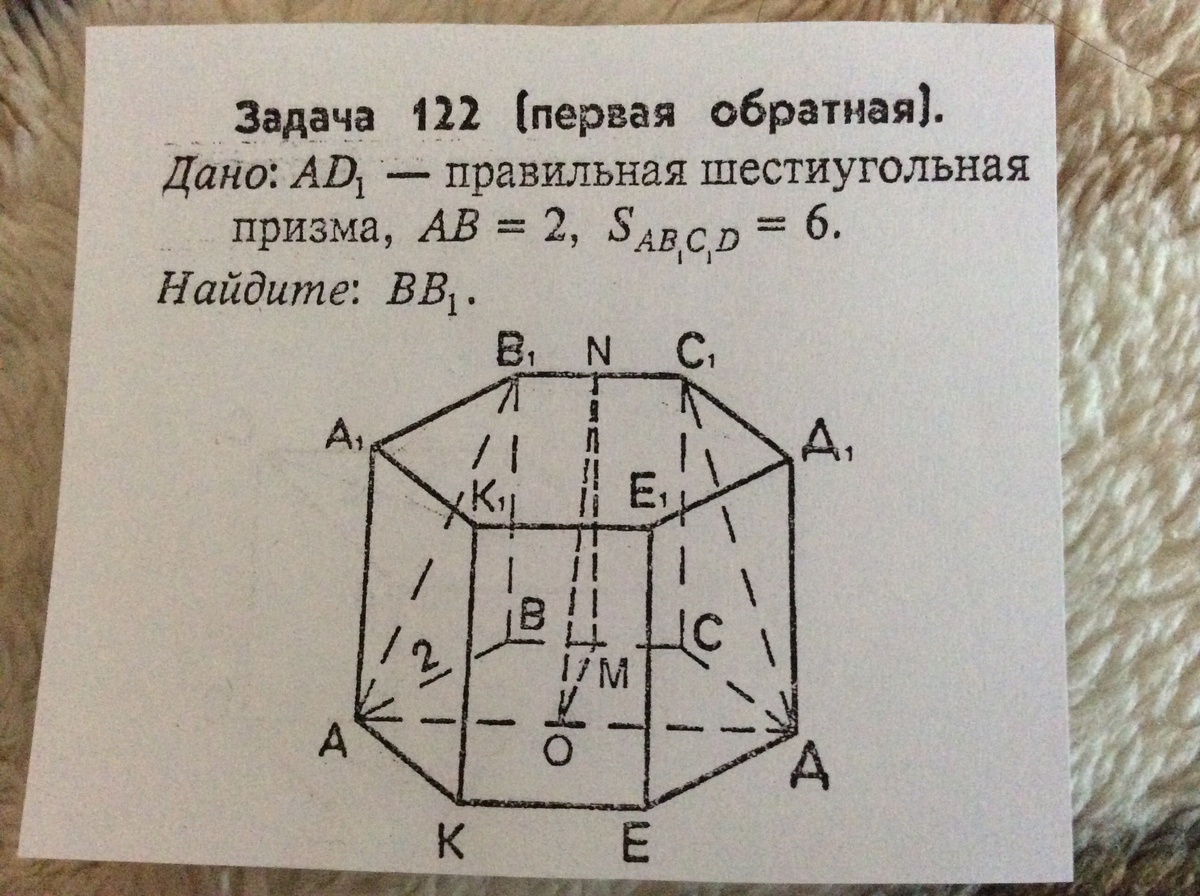
ABCDEKA₁B₁C₁D₁E₁K₁ - правильная шестиугольная призма, АВ=2, площадь АВ₁С₁D=6. Найти ВВ₁. Рисунок есть во вложении

Answer 1

Рассмотрим трапецию AB1C1D
Большее основание = 4 (Длина двух оснований призмы)
Меньшее основание = 2 (Длина призмы)
S=(a+b)h/2 (Площадь трапеции)
6=(4+2)h/2
h=2  (Высота трапеции)
Высота правильного треугольника:
h=a√3/2
h=√3
(Высота призмы, высота правильного треугольника, высота трапеции) образуют
прямоугольный треугольник в котором
Гипотенуза = 2 (Высота трапеции)
Больший катет = √3 (Высота правильного треугольника)
Меньший катет - BB1 (Высота призмы)
ВВ1= √(2²-(√3))=1
Ответ: BB1=1