Question

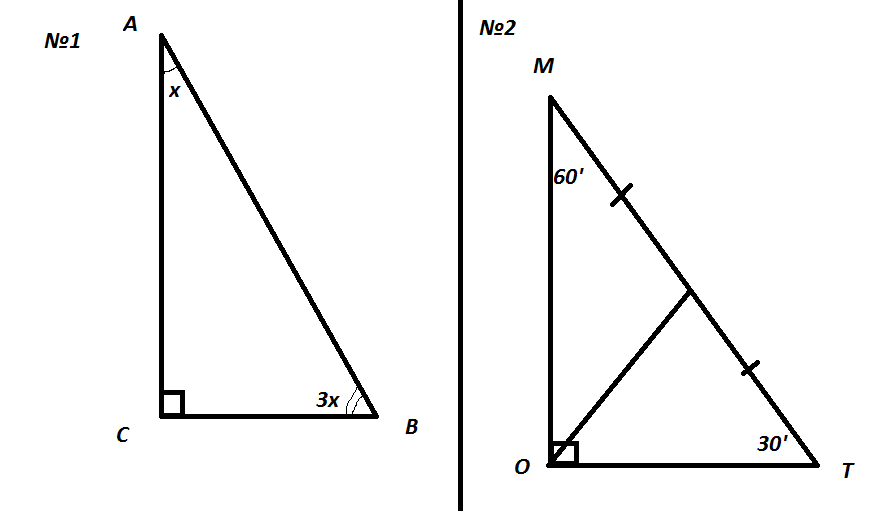
1.В прямоугольном треугольнике один из острых углов в 3 раза больше другого. Найти острые углы этого треугольника.2. В треугольнике МОТ угол О=90*, угол Т=30*. Из угла О проведена медиана ОК к стороне МТ. МО=13 см. Найти длину медианы ОК.

Answer 1

№1. Пусть x'-градусная мера одного острого угла, тогда 3х-градусная мера другого острого угла. Сумма острых углов в прямоугольном треугольнике 90'. 

3х+х=90, отсюда х=22,5', 3x=67,5'. 

Ответ: угол А=22,5', угол B=67,5' 

№2.
Т.к. угол Т=30', то угол М=60' 

МО=2*МТ, т.к. лежит против угла в 30'. Cледовательно, MT=13*2=26. 
МК=КТ=13, т.к. ОК-медиана. 
По теореме Пифагора находим катет ОТ. 
$OT= sqrt{ MT^{2}- MO^{2} }= sqrt{ 26^{2}- 13^{2} } = sqrt{507}=13 sqrt{3}$

Рассмотрим треугольник ОКТ. 

По теореме косинусов найдём ОК: 

$OK= sqrt{13^{2}+(13 sqrt{3})^{2}-2*13*13 sqrt{3}*cos T }=13$

Ответ: ОК=13