Предмет: Геометрия,
автор: Avenger2012
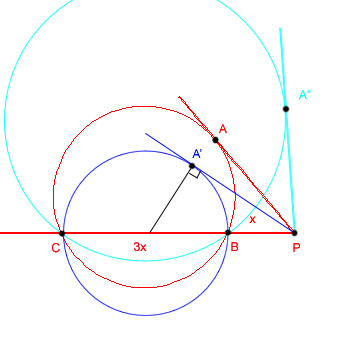
К окружности из точки P проведена касательная PA и секущая, которая пересекает окружность в точках B и C (точка B лежит внутри отрезка PC). Найдите PA, если PC = 8, и PB : BC = 1 : 3.
Ответы
Автор ответа:
0
Предположим, что ВС является диаметром (это ведь не противоречит условию задачи). Тогда в треугольнике OAP (О - центр окружности)
OP = BP + CB/2 = 2 + 6/2 = 5
AO = CB/2 = 3
отсюда AP = корень(OP^2 - AO^2) = 4
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Қазақ тiлi,
автор: ajnuramangeldy235
Предмет: Экономика,
автор: 15Aisha15
Предмет: Геометрия,
автор: mavzuna