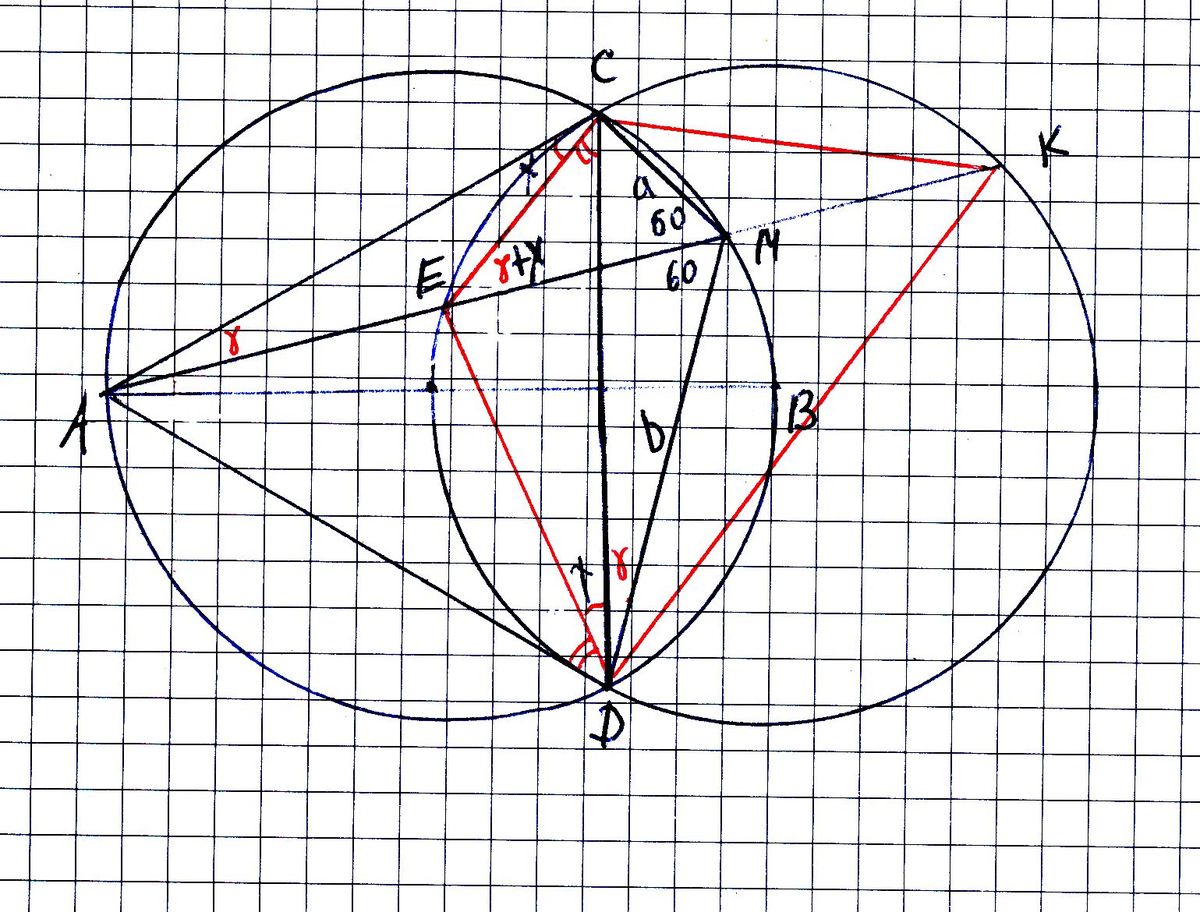
в окружности проведен диаметр AB. Другая окружность с центром B пересекает первую в точках C и D, M-точка первой окружности внутри второй. Отрезок AM пересекает вторую окружность в точке Е. Найдите ME, если MC=a, MD=b.
Ответы
Я набрал решение к этой задаче, полчаса потратил, а все пропало куда-то, чертеж прыгнул в другую задачу. Бред какой-то.
Треугольник АВС прямоугольный, так как АВ - диаметр. Кроме того, ВС = АВ/2. Поэтому АС - касательная к окружности с центром в точке В, а угол САВ = 30 градусов, угол СВА = 60 градусов.
Точно так же AD - касательная ко второй окружности, и угол BAD = 30; угол ABD = 60
Треугольник ABD - правильный.
Угол АМС = угол АВС - оба опираются на дугу АС первой окружности.
Угол АМС = 60 градусов
Точно так же угол AMD = 60 градусов.
Углы САМ и CDM опираются на дугу СМ первой окружности, поэтому они равны.
Угол ЕDC опирается на дугу CE второй окружности (с центром в В), а угол АСЕ - это угол между касательной СА и хордой СЕ дуги СЕ. Поэтому он равен углу EDC.
Осталось заметить, что угол СЕМ = угол САМ + угол АСЕ = угол СDM + угол EDC = угол EDM.
Легко видеть, что в треугольниках СЕМ и DEM есть 2 пары равных углов (причем одна пара - это углы в 60 градусов)
Поэтому треугольники СЕМ и DEM подобны, и МС/ME = ME/MD; ME^2 = a*b