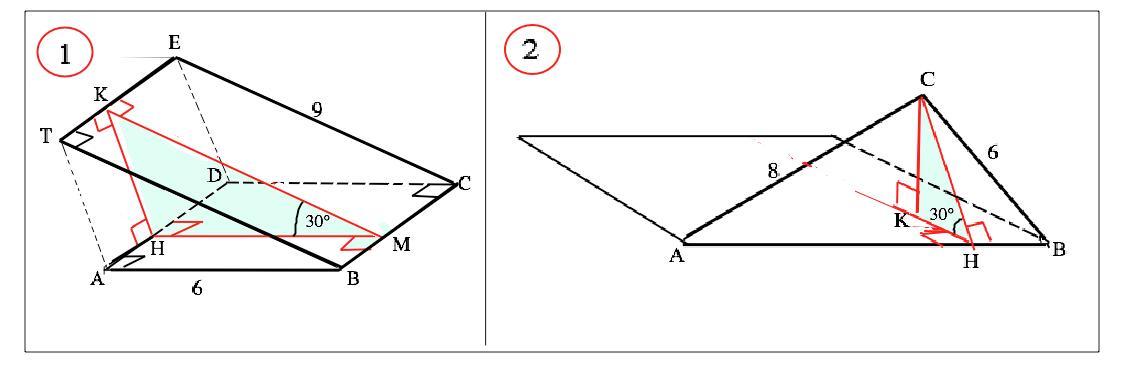
1.
Квадрат
и прямоугольник ,площади которых соответственно равны 36 см2 и 54 см2,имеют общую сторону ,а
угол между их плоскостями равен 300. Найдите расстояние между
параллельными сторонами прямоугольника и квадрата
2.
Через
гипотенузу АВ прямоугольного треугольника АВС
проведена плоскость, образующая с
плоскостью треугольника угол 300.
Найдите расстояние от вершины
С до этой плоскости ,если катеты
треугольника равны 6 см и 8 см
Ответы
Объяснение: (см. рисунки приложения)
1) Угол между плоскостями – двугранный угол. Его величина определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём.
Обозначим квадрат АВСD, прямоугольник ТВСЕ. Ребром угла между их плоскостями является их общая сторона ВС.
КМппВС, МНппВС. Плоскость, содержащая угол 30°, перпендикулярна плоскостям обеих граней.
АD||ВС, ТЕ||ВС ⇒ ТЕ||AD. Искомой расстояние - длина перпендикулярного им отрезка КН между ними.
Длина общей стороны ВС данных фигур - сторона квадрата, поэтому ВС=√S=√36=6 см. НМ=АВ=6 см, КМ=ТВ=9 см. т.к. параллельны им и пересекаются с противоположным сторонами прямоугольников под прямым углом.
По т.косинусов КН²=КМ²+НМ²-2КМ•НМ•cos30°
КН²=36+81-2•6•9•√3/2, откуда КН=√(117-54√3)=≈14,51 см
==============
2) Расстояние от точки до плоскости измеряется длиной отрезка, проведенного между ними перпендикулярно, следовательно, СК⊥КН. Угол 30° образуют НС и НК, перпендикулярные АВ в т.Н. Прямая, перпендикулярная плоскости, перпендикулярна любой прямой в плоскости, проходящей через ее основание.. СК перпендикулярна плоскости, СК - искомое расстояние.
СК=СН•sin30°, или, как катет ∆ СКН, противолежащий углу 30°, СК равен половине гипотенузы СН.
Соотношение катетов треугольника 3а:4а, следовательно ∆ АВС - египетский. a=8:4=2; АВ=5а=10 см
В ∆ АВС его высота CH=AC•ВС:АВ=48:10=4,8 см. ⇒ СК=4,8•1/2=2,4 см