Question

Помогите с геометрией
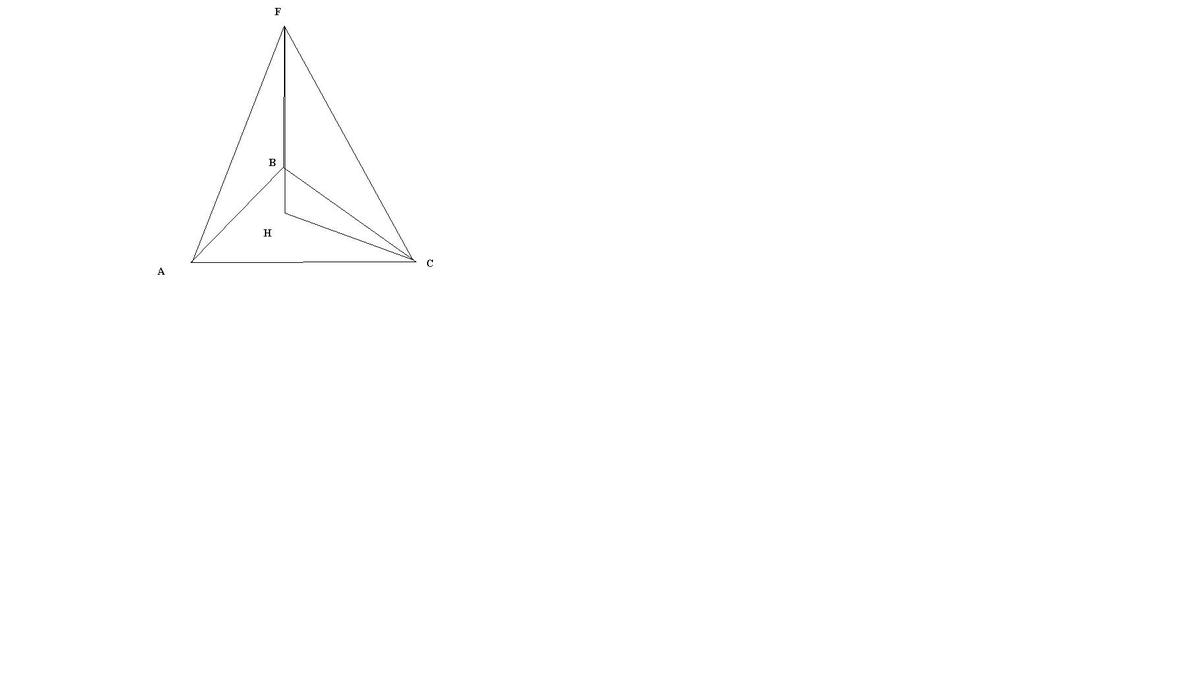
Высота правильной треугольной пирамиды равна 8 см. Радиус окружности, описанной около ее основания-8 корней из 3. Вычислить: а) длину бокового ребра пирамиды Б) площадь боковой поверхности пирамиды.
ЧЕРТЕЖ ОБЯЗАТЕЛЕН, так как не всегда ваши буквенные обозначения совпадают с моими

РЕШЕНИЕ С ОТСЫЛКОЙ К ТЕОРИИ И ОБЬЯСНЕНИЯМИ

Answer 1

Если опустим высоту , тогда получим прямоугольный треугольник $FHC$.
Откуда ребро $FC=sqrt{(8sqrt{3})^2+8^2}=16$ 
Опустим высоту боковой грани , найдем сторону треугольника пусть она  равна $a$    , тогда     $8sqrt{3}=frac{sqrt{3}a}{3}\ a=24$ , откуда высота $h=sqrt{16^2-frac{24}{2}} = 4sqrt{7}\ S=frac{24*3*4sqrt{7}}{2}=144sqrt{7}$