Предмет: Алгебра,
автор: bot1234
помогите доказать неравенства. номер 1070
Приложения:
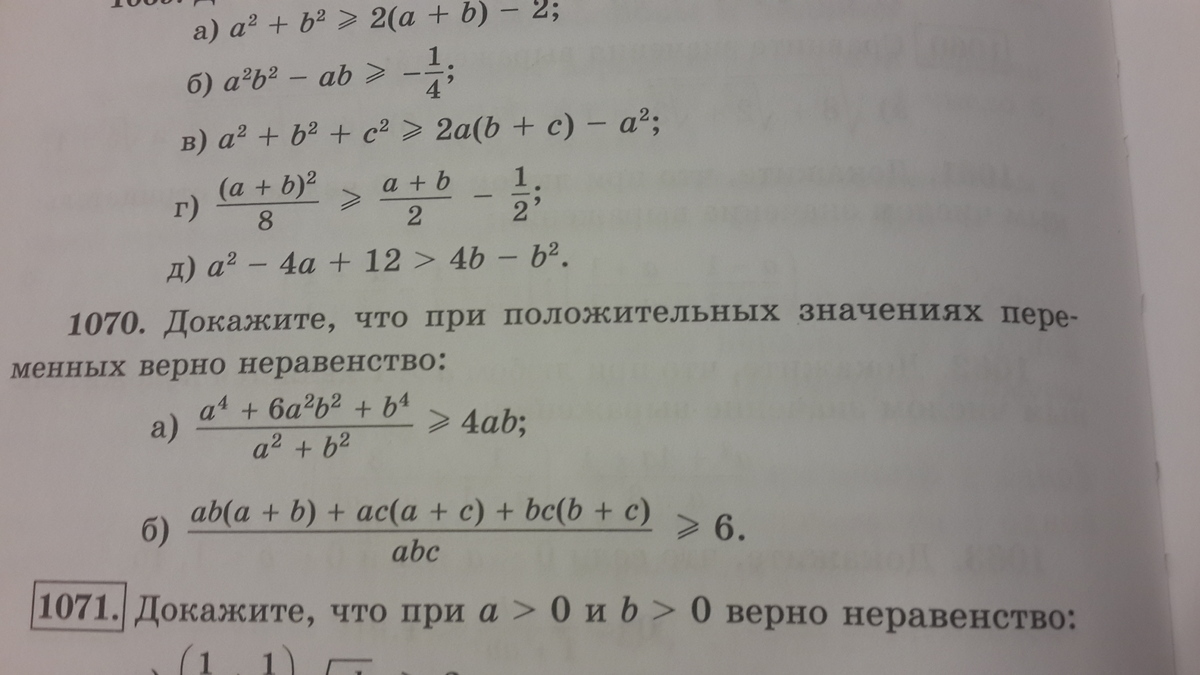
Ответы
Автор ответа:
0
Верно
Используем неравенство между средними
Похожие вопросы
Предмет: Английский язык,
автор: asel12344412
Предмет: Қазақ тiлi,
автор: daniiarmalgazhdar10
Предмет: Физкультура и спорт,
автор: arustvv
Предмет: Математика,
автор: Аноним
Предмет: Геометрия,
автор: ариночкааа