Предмет: Алгебра,
автор: anechkashad
cos2x+(корень из 2) *sinx=1, число корней на интервале (-3:2)
Ответы
Автор ответа:
0
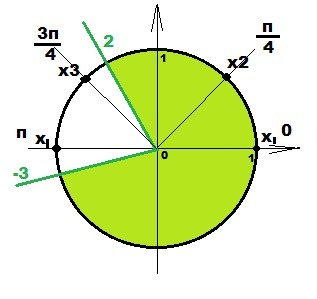
1) sin x = 0; x₁ = πk; x₁ ≈ 3,14k; k∈Z
2) 1 - √2 sin x = 0; sin x = 1/√2 = √2 /2;
x₂ = π/4 + 2πn; x₂ ≈ 0,79 + 6,28*n; n∈Z
x₃ = 3π/4 + 2πm; x₃ ≈ 2,36 + 6,28*m; m∈Z
Проверка интервала
1) -3 < x₁ < 2 ⇔ -3 < 3,14k < 2
-0,95 < k < 0,64
k = 0 ⇒ x₁ = π*0 = 0;
2) -3 < x₂ < 2 ⇔ -3 < 0,79 + 6,28*n < 2
-3,79 < 6,28*n < 1,21
-0,6 < n < 0,19
n = 0 ⇒ x₂ = π/4 + 2π*0 = π/4;
3) -3 < x₃ < 2 ⇔ -3 < 2,36 + 6,28*m < 2
-5,36 < 6,28*m < -0,36
-0,85 < m < -0,06 Целых значений m нет
Ответ: в интервал (-3; 2) попадают два корня : x₁ = 0; x₂ = π/4.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: anna300107
Предмет: Химия,
автор: valerismart12
Предмет: Литература,
автор: ommaro870
Предмет: Математика,
автор: герда778