Предмет: Алгебра,
автор: bastish
Докажите, что уравнение (на фото) имеет корень равный 1, а других корней у него нет
Приложения:
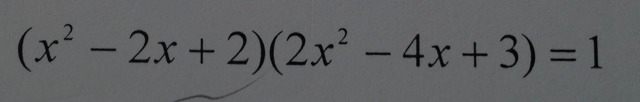
Ответы
Автор ответа:
0
(x²-2x+2)(2x²-4x+3)=1
(x²-2x+2)(2(x²-2x)+3)=1
Замена: a=x²-2x
(a+2)(2a+3)=1
2a²+4a+3a+6-1=0
2a²+7a+5=0
D=7²-4*2*5=49-40=9=3²
a1=(-7+3)/4=-1
a2=(-7-3)/4=-2,5
x²-2x=-1 x²-2x=-2,5
x²-2x+1=0 x²-2x+2,5=0
(x-1)²=0 D=(-2)²-4*1*2,5=4-10=-6<0
x-1=0 решений нет
x=1
Таким образом. доказано, что уравнение имеет единственное решение х=1
(x²-2x+2)(2(x²-2x)+3)=1
Замена: a=x²-2x
(a+2)(2a+3)=1
2a²+4a+3a+6-1=0
2a²+7a+5=0
D=7²-4*2*5=49-40=9=3²
a1=(-7+3)/4=-1
a2=(-7-3)/4=-2,5
x²-2x=-1 x²-2x=-2,5
x²-2x+1=0 x²-2x+2,5=0
(x-1)²=0 D=(-2)²-4*1*2,5=4-10=-6<0
x-1=0 решений нет
x=1
Таким образом. доказано, что уравнение имеет единственное решение х=1
Похожие вопросы