Question

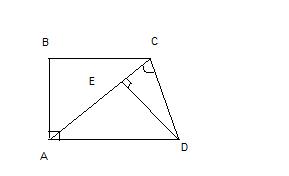
В трапеции ABCD угол A = 90 градусов, AC = 6 корней квадратных из 2, BC = 6, DE - высота треугольника ACD, а tg угла ACD = 2. Найдите CE

Answer 1

1. По теореме Пифагора найдем неизвестный катет АВ в прямоугольном треугольнике АВС:
АВ=√AC² - BC² =√(6√2)²- 6² = √36*2-36=√36=6
Получаем, что треугольник АВС - равнобедренный, значит углы при его основании АС равны:
<BAC=<BCA=(180-90):2=45°
2. <BCA=<CAD как накрест лежащие углы при пересечении двух параллельных прямых ВС и AD секущей АС,<CAD=45°
3. Треугольники АВС и AED подобны по первому признаку подобия: два угла одного треугольника соответственно равны двум углам другого. В нашем случае:<B=<AED=90°, <BCA=CAD=45°
4. Зная тангенс угла ACD запишем:
tg ACD = ED/EC, отсюда EC=ED/tg ACD= ED/2
5. Для подобных треугольников можно записать:
AB:AE=BC:ED. 
AE=AC-EC=6√2-ED/2, AE=$frac{12 sqrt{2} - ED}{2}$. Запишем отношение для подобных треугольников как:
$6: frac{12 sqrt{2}-ED }{2}=6:ED$
$frac{12}{12 sqrt{2} -ED} = frac{6}{ED}$
ED=4√2
6. ЕС=ED/2=4√2/2=2√2