Question

Решите пожалуйста задачи с этой фотографии

Answer 1

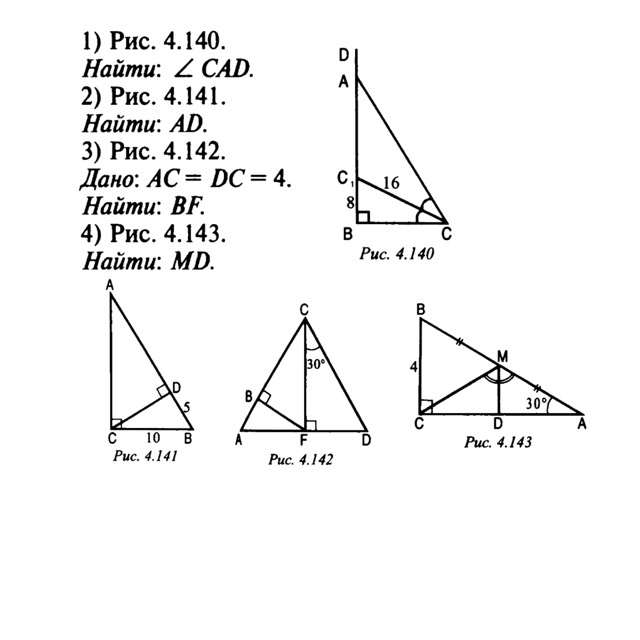
Рис 4.140
sin BCC1=BC/CC1=8/16=1/2, значит
<BCC1=30°
В треугольнике АВС
 <C=<BCC1*2=30*2=60°
Зная, что сумма углов треугольника равна 180°, находим угол САВ:
<CAB= 180-<B-<C=180-90-60=30°
Зная, что развернутый угол DAB равен 180°, находим внешний угол CAD:<CAD=180-<CAB=180-30=150°

Рис. 4.141
В прямоугольном треугольнике BCD по теореме Пифагора находим CD:
CD=√CB² - BD²= √10² - 5² = √75=√25*3=5√3
В прямоугольном треугольнике АВС
CD=√BD*AD, отсюда
AD=СD²/BD=(5√3)²/5=15

Рис. 4.142
В прямоугольном треугольнике  FCD катет, лежащий против угла в 30°, равен половине гипотенузы. Значит
FD=1/2CD=1/2*4=2
Поскольку в равнобедренном треугольнике высота CF является и медианой, то FD=AF=2
В прямоугольном треугольнике ACF катет AF - среднее пропорциональное для гипотенузы АС и его проекции АВ на гипотенузу:
AF=√AB*AC, отсюда
AB=AF²/AC= 2²/4=1
По теореме Пифагора находим BF в прямоугольном треугольнике ABF:
BF=√AF² - AB² = √2² - 1² =√3

Рис. 4.143
В прямоугольном треугольнике АВС катет ВС, лежащий против угла 30°, равен половине гипотенузы АВ:
АВ=2*СВ=2*4=8
М - середина АВ, значит ВМ=АМ=4 и треугольник ВСМ - равнобедренный (ВС=ВМ=4)
В треугольнике АВС <B=180-<C-<A=180-90-30=60°
Поскольку ВСМ - равнобедренный, то углы ВСМ и ВМС при его основании равны:<BCM=<BMC=(180-<B):2=(180-60):2=60°
Все углы треугольника ВСМ по 60°, значит ВСМ - равносторонний, и СМ=4
В треугольнике АСМ:
СМ=АМ=4, он - равнобедренный, и MD - не только биссектриса, но и медиана тоже, значит точка D - середина АС.
Таким образом, MD  - средняя линия треугольника АВС, поскольку соединяет середины сторон. Средняя линия параллельна ВС и равна половине этой стороны:
MD=1/2BC=1/2*4=2