Question

Хорда, перпендикулярная диаметру, делит его на отрезки, разность которых равна 7 см. Найдите радиус окружности, если длина хорды равна 24 см.

Answer 1

1) Пусть диаметр АВ и хорда СД пересекаются в точке К. Хорда, перпендикулярная диаметру, поэтому СК=КД = 24/2 =12см
2) По свойству пересекающихся хорд 
СК*КД = АК*КД или 12*12 = х(х+7) , где АК=х
3) тогда х² +7х -144 =0 или х= 9см
4) КВ =9+7 =16см
5) Д = 2R =16+9 = 25см поэтому R= 25/2 = 12,5 см

Answer 2

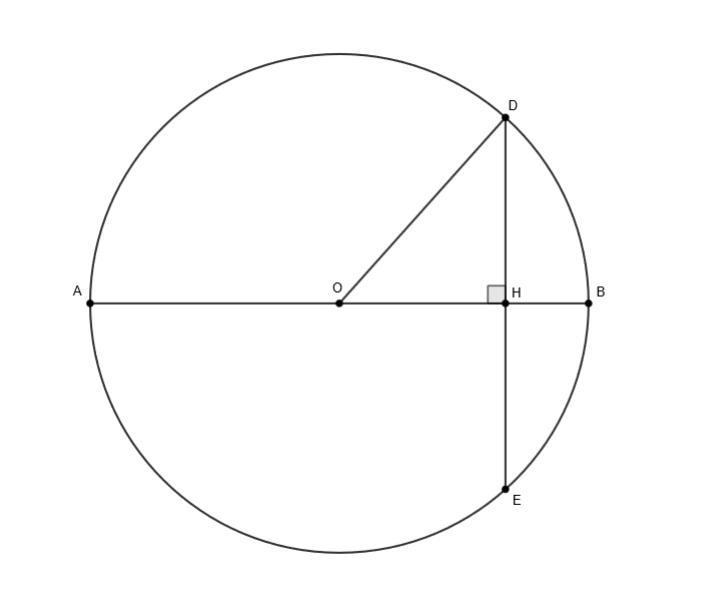
1 способ:  Пусть HB = х,  AH - HB = 7  ⇒  AH = x + 7

AB = AH + HB = x + (x + 7) = 2x + 7

AO = OB = AB/2 = (2x + 7)/2

OH = OB - HB = (2x + 7)/2  -  x = 7/2 = 3,5 см

Теорема: Хорда, перпендикулярная диаметру, делится пополам.

DH = HE = DE/2 = 12 см

По т. Пифагора:

OD² = OH² + HD² = (7/2)² + 12² = 625/4

OD = 25/2 = 12,5

2 способ: Теорема: Для двух пересекающихся хорд верно  равенство

AH * HB = DH * HE

(x + 7) * x = 12 * 12

x² + 7x - 144 = 0

По теореме, обратной т. Виета:  х₁ = - 16  и  х₂ = 9

Значит, НВ = 9, АН = 16  ⇒  AO = OB = AB/2 = 25/2 = 12,5