Предмет: Геометрия,
автор: Наастя23
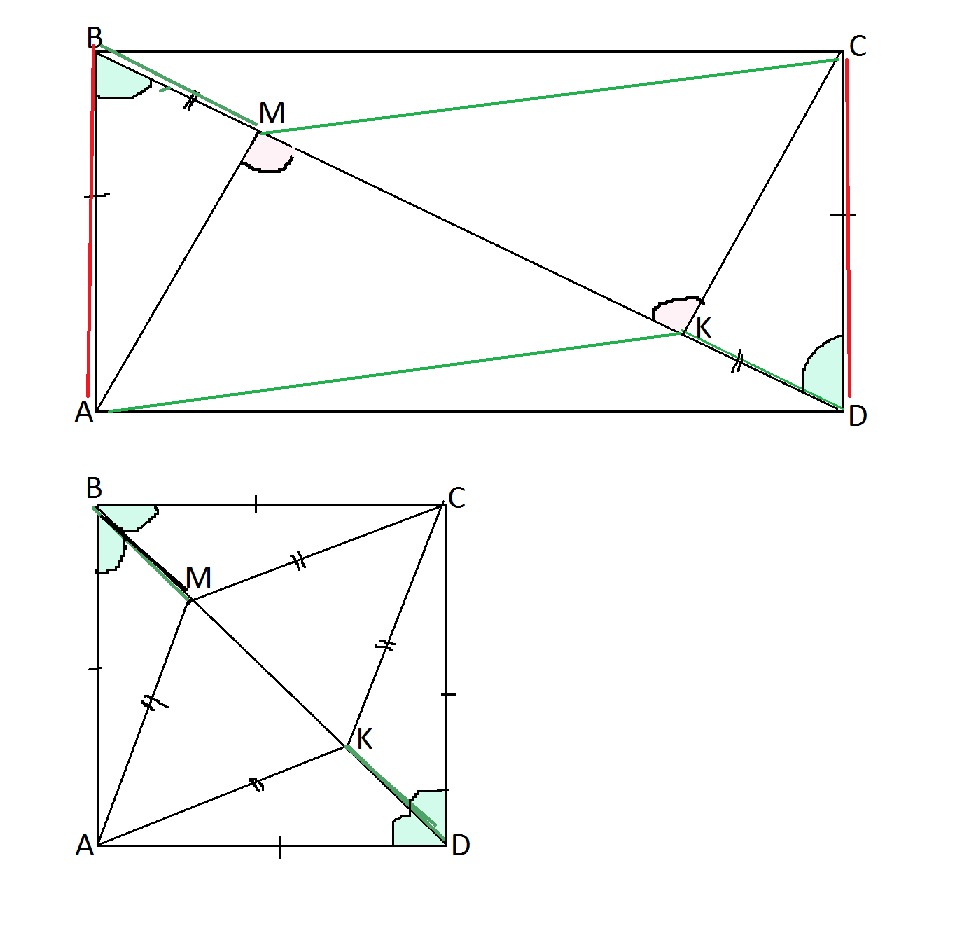
На диагонали ВД прямоугольника АВСД отложены равные отрезки ВМ и ДК. а) Докажите равенство треугольников АВМ и СДК. б) Определите вид четырехугольника АМСК.
Ответы
Автор ответа:
0
ВМ=КД по условию задачи.
ВС=СД как стороны прямоугольника.
угол АВМ равен углу СДК как накрестлежащие при пересечении параллельных прямых секущей.
Эти треугольника равны по двум сторонам и углу между ними.
------------
Получившийся четырехугольник - параллелограмм.
Четырехугольник АМСК составлен из двух треугольников.
Они равны, т.к. углы при М и К равны как дополняющие до 180 градусов углы ВМА и СКD, стороны АМ=СК равны в равных треугольниках, а МК - общая сторона.
Углы при М и К накрестлежащие при пересечении АМ и СК секущей, следовательно, АМ || СК, и параллельность и равенство противоположных сторон четырехугольника - признак параллелограмма.
Четырехугольник АМСК будет ромбом, если исходный прямоугольник - квадрат.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Marusick2020
Предмет: Математика,
автор: angel192121
Предмет: Английский язык,
автор: serpen725
Предмет: Математика,
автор: Svetik13081982